
一、罗尔(Rolle)定理费马(fermat)引理y=f(x)在U(xo)有定义,> f'(xo)= 0且f(x)≤f(xo), f(xo)存在L(或≥)证: 设Vxo +Ax e U(xo), f(xo + △x)≤ f(xo),XoX0f(xo +Ax)- f(xo)则 f'(xo)= limAxAr-0f'(xo)≥0 (△x →0-)>f'(xo)=0f*(xo)≤0 (x→0t)证毕HIGH EDUCATION PRESS
费马(fermat)引理 一、罗尔( Rolle )定理 且 存在 证: 设 则 证毕
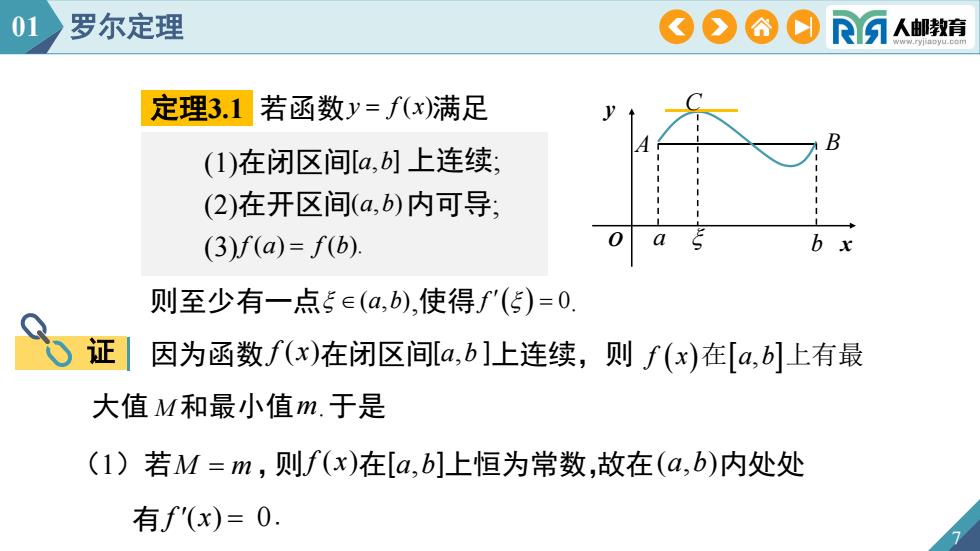
01罗尔定理CORA人邮教育1定理3.1若函数y=f(x)满足B(1)在闭区间[a,b]上连续:(2)在开区间(a,b)内可导:0abx(3)f(a)= f(b)则至少有一点e(a,b),使得f'()=00证因为函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上有最大值M和最小值m.于是(1)若M =m,则f(x)在[a,b]上恒为常数,故在(a,b)内处处有f'(x)= 0
a b A B C x y O 7 定理3.1 若函数y f (x)满足 (1)在闭区间[a,b] 上连续; (2)在开区间(a,b)内可导; (3)f (a) f (b). 则至少有一点 (a,b),使得 f 0. 01 罗尔定理 证 因为函数 f (x)在闭区间[a,b ]上连续,则 大值 M 和最小值m.于是 (1)若M m,则f (x)在[a,b]上恒为常数,故在(a,b)内处处 有 f (x) 0. f x在a,b上有最

01罗尔定理OOOORA人邮教育(2)若M >m,因f(a)=f(b),则m与M中至少有一个不等于端点的函数值不妨设M±f(a),即最大值不在两个端点处取得,则在(a,b)内至少存在一点使得f()= M.由费马引理得,f"()=0
8 01 罗尔定理 不妨设M f (a),即最大值不在两个端点处取得,则在(a,b) 内至少存在一点, 由费马引理得: 使得f ( ) M. 由费马引理得, (2)若M m,因 f (a) f (b),则m与M中至少有一个不等于端点的函数值, f 0
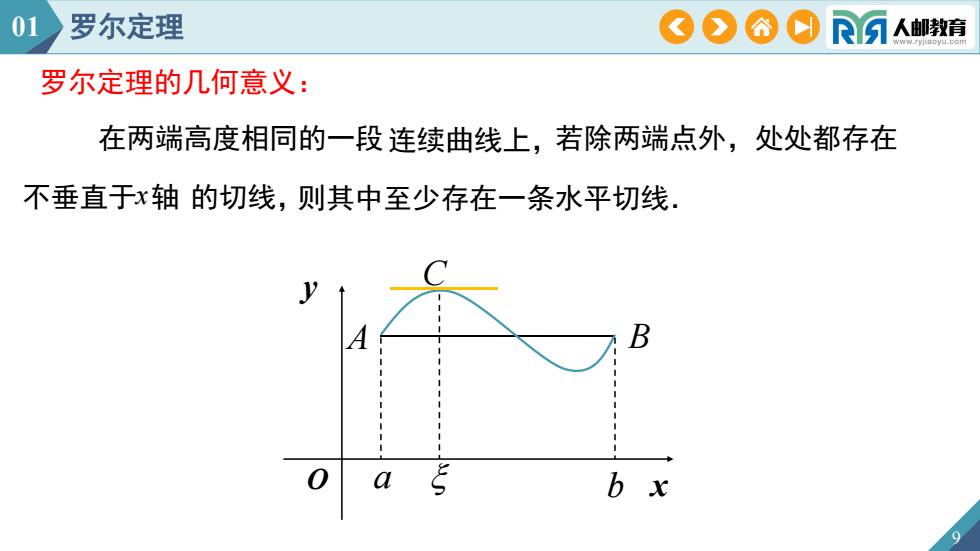
01罗尔定理COA0R人邮教育罗尔定理的几何意义:在两端高度相同的一段连续曲线上,若除两端点外,处处都存在不垂直于x轴的切线,则其中至少存在一条水平切线,B0abx
9 的切线, 在两端高度相同的一段连续曲线上, x 若除两端点外,处处都存在 a b A B C x y O 则其中至少存在一条水平切线. 01 罗尔定理 罗尔定理的几何意义: 不垂直于 轴

01罗尔定理COOORA人邮教育罗尔定理的代数意义是:当f(x)可导时,在函数f(x)的两个等值点之间至少存在方程(x)=0的一个根.注(1)定理中的不唯一,定理只表明的存在性;(2)定理的条件是结论成立的充分条件而非必要条件即条件满足时结论一定成立,若条件不满足,结论可能成立也可能不成立
10 注 (1) 定理中的 ξ 不唯一,定理只表明ξ的存在性; (2) 定理的条件是结论成立的充分条件而非必要条件. 成立也可能不成立. 即条件满足时结论一定成立,若条件不满足,结论可能 01 罗尔定理 两个等值点之间至少存在方程 f (x) 0 的一个根. 罗尔定理的代数意义是:当 f (x)可导时,在函数 f (x)的