则该性质3.若行列式中某行元素为两数和,行列式可拆成相应的两个行列式的和331n-2 + 54+71Ain +b.ai, +biz...Ai +b,1323+21+616+.7-2 +5-214 + 7a.annnala12aua2?nVbb,b;2ai22unilinaaa0n2nlnnnln2nn加油!
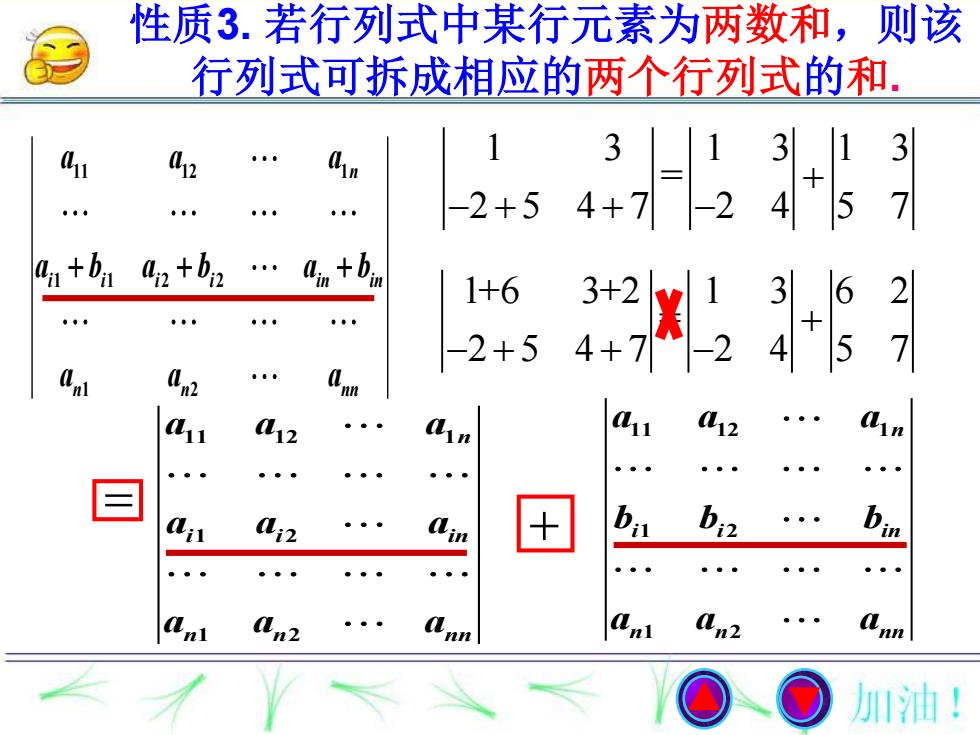
性质3. 若行列式中某行元素为两数和,则该 行列式可拆成相应的两个行列式的和. 11 12 1 1 1 2 2 1 2 n i i i i in in n n nn a a a a b a b a b a a a 11 12 1 1 2 1 2 n i i in n n nn a a a a a a a a a 11 12 1 1 2 1 2 n i i in n n nn a a a b b b a a a 1 3 1 3 1 3 = 2 5 4 7 2 4 5 7 1+6 3+2 1 3 6 2 = 2 5 4 7 2 4 5 7
相等 D=DI性质1.行列式D与其转置行列式DT将行列式的行与列互换,就得到其转置行列式。a?0211nlCa1201n22n2qa1ann2nlnnn行列式中行与列具有同等的地位凡是对行成立性质的对列也同样成立加油!
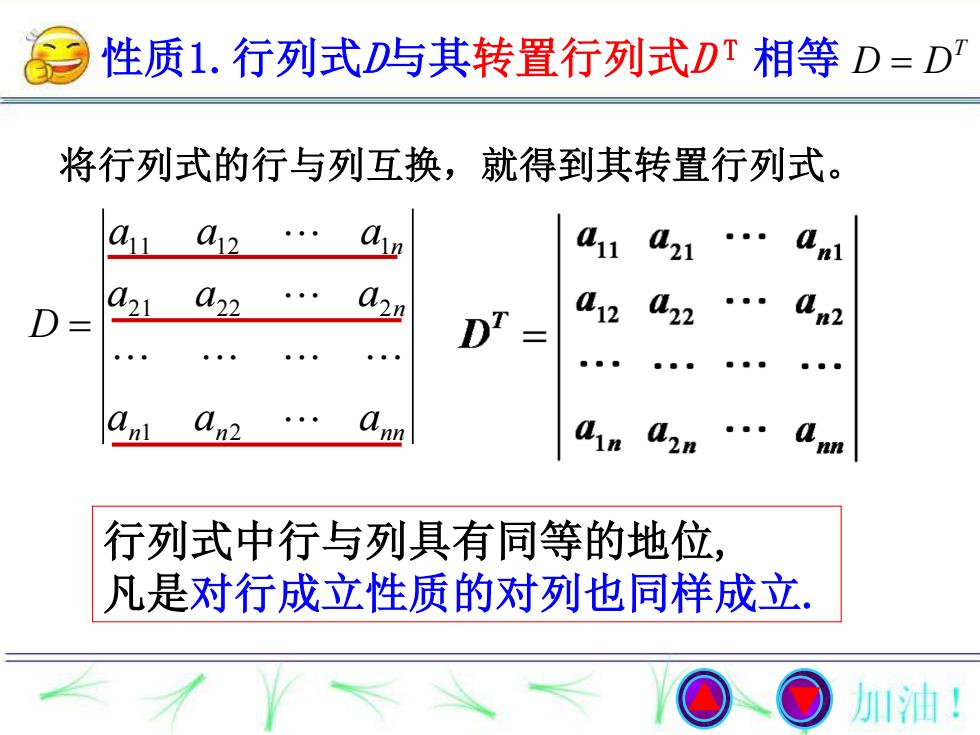
性质1.行列式D与其转置行列式D T 相等 n n nn n n a a a a a a a a a D 1 2 21 22 2 11 12 1 将行列式的行与列互换,就得到其转置行列式。 行列式中行与列具有同等的地位, 凡是对行成立性质的对列也同样成立. T D D
3211134243172018043-5-58724-1-1加油!
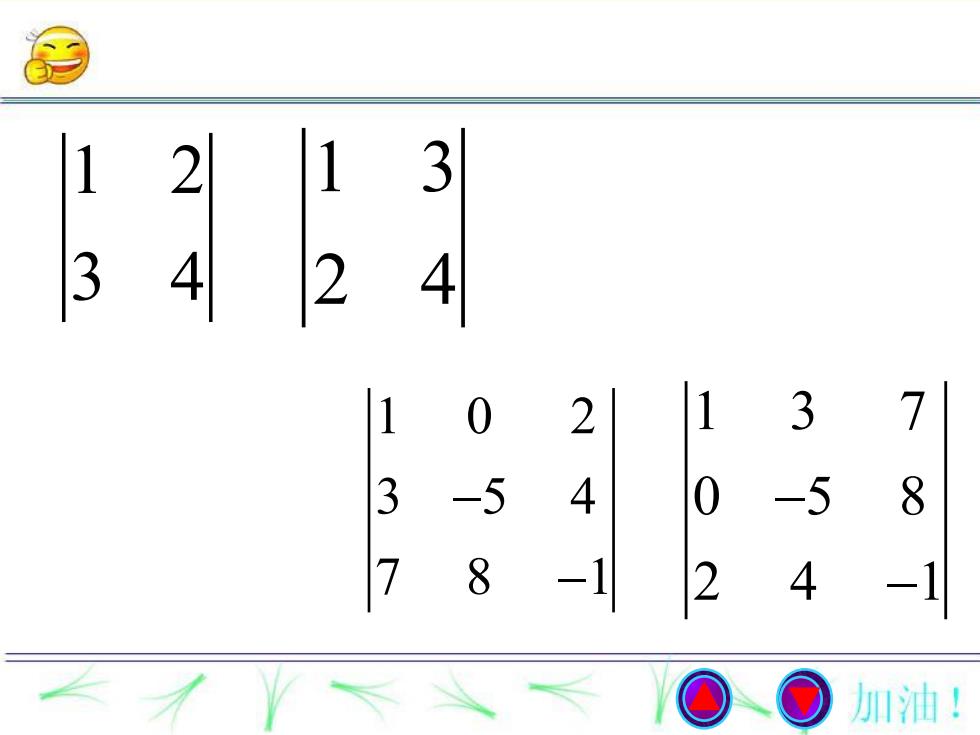
1 2 3 4 1 3 2 4 1 0 2 3 5 4 7 8 1 1 3 7 0 5 8 2 4 1

性质4(行列式的初等变换)若把行初等变换施于n阶行列式上则:(1)将A的某一行乘以数k得到A,则detA, = k(detA);(2) 将A的某一行的k(+0)倍加到另一行得到A2,则detA, = detA;(3)交换A的两行得到A3,则 detA,=-detA.加油!
性质4(行列式的初等变换)若把行初等 变换施于n阶行列式上则: (1) 将A的某一行乘以数k得到A1,则 detA1 = k(detA); (2) 将A的某一行的k(≠0)倍加到另一行得到A2 ,则 detA2 = detA; (3) 交换A的两行得到A3 , 则 detA3 = - detA

(1)将A的某一行乘以数k得到A,,则 detA,=k(detA);aYnkkaKaila;2Cininanaaaaan2n2nnnlnn行列式某一行的所有元素都乘以同一数k,等于用数k乘以此行列式。加油!
n n nn i i in n a a a ka ka ka a a a 1 2 1 2 11 12 1 n n nn i i in n a a a a a a a a a 1 2 1 2 11 12 1 k (1)将A的某一行乘以数k得到A1,则 detA1 = k(detA); 行列式某一行的所有元素都乘以同一数k, 等于用数k乘以此行列式