
微训练2为了得到y=sin4x,x∈R的图象,只需把正弦曲线上 所有点的( A.横坐标伸长到原来的4倍,纵坐标不变 B横坐标缩短到原来的,纵坐标不变 C.纵坐标伸长到原来的4倍,横坐标不变 D.纵坐标缩短到原来的,横坐标不变 答案:B 解析:ω=4>1,因此只需把正弦曲线上所有点的横坐标缩短到 原来的,纵坐标不变
导航 微训练2 为了得到y=sin 4x,x∈R的图象,只需把正弦曲线上 所有点的( ) A.横坐标伸长到原来的4倍,纵坐标不变 B.横坐标缩短到原来的 ,纵坐标不变 C.纵坐标伸长到原来的4倍,横坐标不变 D.纵坐标缩短到原来的 ,横坐标不变 答案:B 解析:ω=4>1,因此只需把正弦曲线上所有点的横坐标缩短到 原来的 ,纵坐标不变. 𝟏 𝟒 𝟏 𝟒 𝟏 𝟒
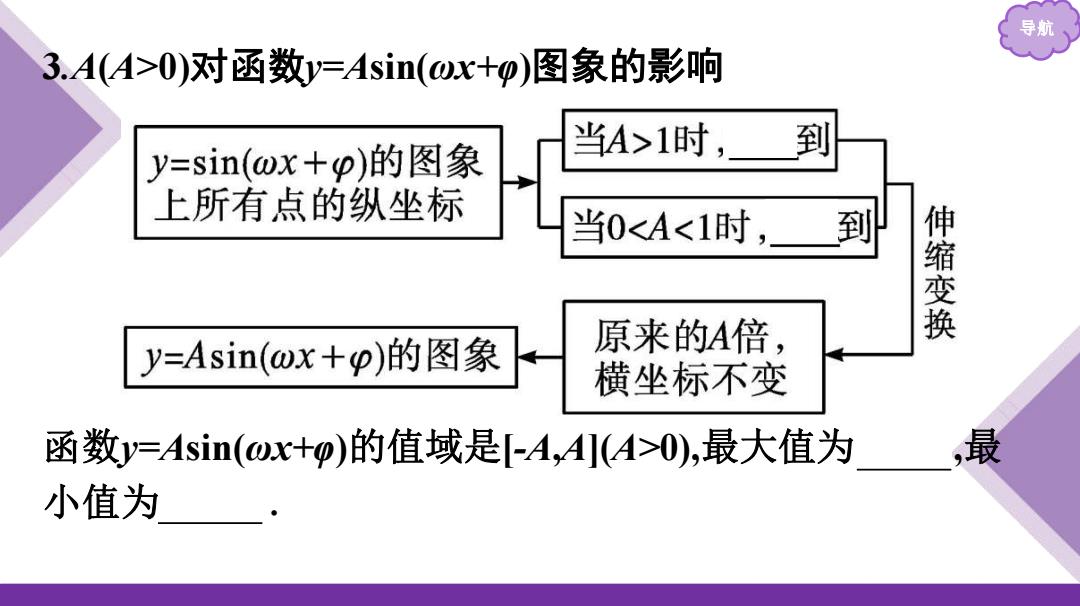
导 3.A(A>0)对函数y=Asin(wx+p)图象的影响 y=sin(wx+p)的图象 当A>1时, 到 上所有点的纵坐标 当0<A<1时, 到 伸缩变换 y=Asin(ωx+p)的图象 原来的A倍, 横坐标不变 函数y=Asin(ox+p)的值域是[-A,A(A>0),最大值为 最 小值为
导航 3.A(A>0)对函数y=Asin(ωx+φ)图象的影响 函数y=Asin(ωx+φ)的值域是[-A,A](A>0),最大值为 A ,最 小值为 -A

导航 微训练3把函数y=2sin3x图象上所有点的横坐标变为原来的 2倍,纵坐标变为原来的3倍,得到函数 的图象 答案y6sin2x
导航 微训练3 把函数y=2sin 3x图象上所有点的横坐标变为原来的 2倍,纵坐标变为原来的3倍,得到函数 的图象. 答案:y=6sin x 𝟑 𝟐

导 4.一 般地,函数y=Asin(wx+p)A>0,w>0)的图象,可以用下面的 方法得到:先画出y=snx的图象;再把正弦曲线向左(或右)平 移 个单位长度,得到函数y=sinc+p)的图象;然后把曲 线上各点的横坐标变为原来的 倍(纵坐标不变),得到函数 y=sin(ox+p)的图象;最后把曲线上各点的纵坐标变为原来的 倍(横坐标不变),这时的曲线就是函数y=Asin(wx+p)的 图象
导航 4.一般地,函数y=Asin(ωx+φ)(A>0,ω>0)的图象,可以用下面的 方法得到:先画出y=sin x的图象;再把正弦曲线向左(或右)平 移 |φ| 个单位长度,得到函数y=sin(x+φ)的图象;然后把曲 线上各点的横坐标变为原来的 倍(纵坐标不变),得到函数 y=sin(ωx+φ)的图象;最后把曲线上各点的纵坐标变为原来的 A 倍(横坐标不变),这时的曲线就是函数y=Asin(ωx+φ)的 图象. 𝟏 𝝎

微训练4已知曲线C=cosx,C2:=sin(2x+),则下面结 论正确的是( A.把C1,上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得 到的曲线向右平移:个单位长度,得到曲线C2 B.把C上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得 到的曲线向左平移亚个单位长度,得到曲线C, C把C1上各点的横坐标缩短到原来的,纵坐标不变,再把得到 的曲线向右平移:个单位长度,得到曲线C2 D.把C,上各点的横坐标缩短到原来的,纵坐标不变,再把得 到的曲线向左平移2个单位长度,得到曲线C
导航 微训练4 已知曲线C1 :y=cos x,C2 : ,则下面结 论正确的是( ) A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得 到的曲线向右平移 个单位长度,得到曲线C2 B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得 到的曲线向左平移 个单位长度,得到曲线C2 C.把C1上各点的横坐标缩短到原来的 ,纵坐标不变,再把得到 的曲线向右平移 个单位长度,得到曲线C2 D.把C1上各点的横坐标缩短到原来的 ,纵坐标不变,再把得 到的曲线向左平移 个单位长度,得到曲线C2 y=sin 𝟐𝒙 + 𝟐𝛑 𝟑 𝛑 𝟔 𝛑 𝟏𝟐 𝟏 𝟐 𝛑 𝟔 𝟏 𝟐 𝛑 𝟏𝟐