3.极值的充分条件极值的一阶充分条件定理2(第一充分条件)一设f(x)在x点连续,且在xo的某去心邻域 U(xo,)内可导。(1)若当x E(x -S,x)时,f'(x)>0(<0);当x E (xo,X +8)时,f'(x)<0 (>0),则f(x,)为极大值 (极小值);(2)若f(x)在x,附近不变号则 f(x)不是极值,y2totXoXoxx
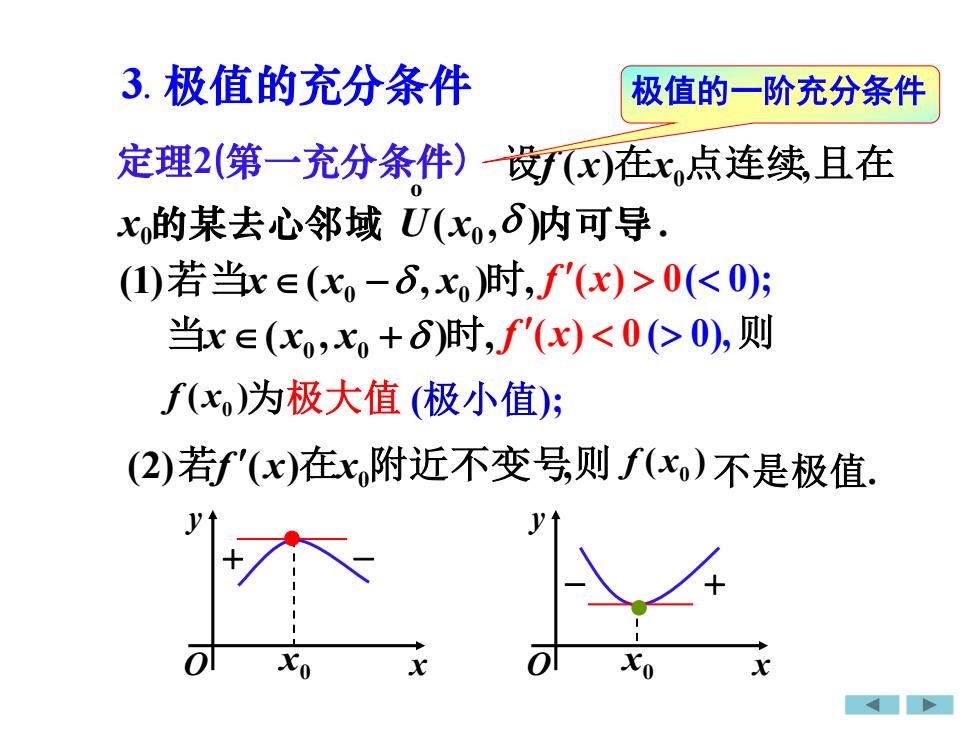
定理2(第一充分条件) 设f (x)在x0 点连续,且在 (1) ( , ) , 若当x x0 − x0 时 f (x) 0( 0); ( , ) , 当x x0 x0 + 时 f (x) 0 ( 0), 则 ( ) x0 f 为极大值 (2) ( ) , 若f x 在x0 附近不变号 ( ) x0 则 f 不是极值. (极小值); 极值的一阶充分条件 x y O x0 • + − x y O x0 − + • ( , ) . 0 o x0的某去心邻域 U x 内可导 3. 极值的充分条件
不是极值点olotXoXoxx般求极值的步骤(1)求导数;2)求驻点与不可导点;③)求相应区间的导数符号,判别增减性:(4)求极值
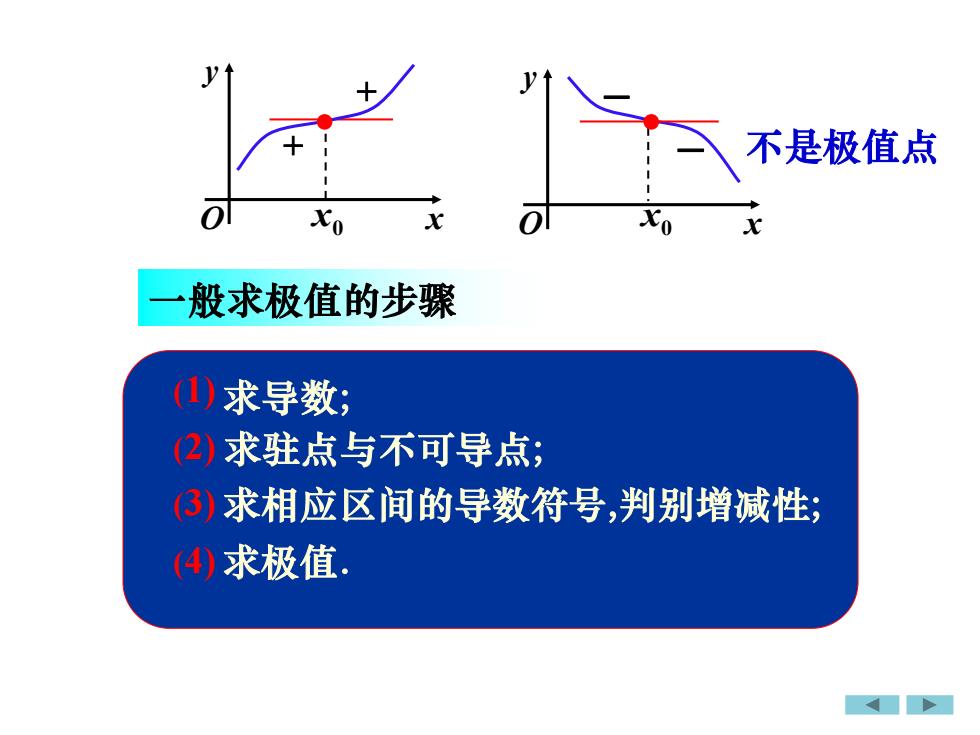
x0 x0 + − − + 一般求极值的步骤 求导数; 求驻点与不可导点; 求相应区间的导数符号,判别增减性; 求极值. (1) (2) (3) (4) 不是极值点 • • x y O x y O

2例1求 f(x)=(x+1)(x-1)3 的极值及单调区间解 (1) f'(x)=3(x+1)(x-1)3 +=(x+1)(x-1)3(x +1)(11x - 7)3(x-1)37(2)驻点:x =-1,x=导数不存在的点:x=1.11(3)列表:求相应区间的导数符号,判别增减性确定极值点和极值
例1 解 ( ) ( 1) ( 1) . 3 2 求 f x = x + 3 x − 的极值及单调区间 3 2 2 f (x) = 3(x + 1) (x −1) 3 1 3 ( 1) ( 1) 3 2 − + x + x − 3 1 2 3( 1) ( 1) (11 7) − + − = x x x (1) (2)驻点: x = −1, 导数不存在的点: . 11 7 x = x = 1. (3)列表:求相应区间的导数符号,判别增减性, 确定极值点和极值
求 f(x)=(x+1)(x-1)3 的极值及单调区间7(x +1)°(11x - 7)驻点:x=-1,x=11f'(x) =3(x -1)3导数不存在的点:x=11(-11)1-1()x(-00,-1)(1,+8)1i+f(x)00++不存在非极值极小值极大值f(x)极小值f(1)=0极大值f(~2.2单调增加区间:(-0,-11,[-1,引], [1,+),单调减少区间:,1)一
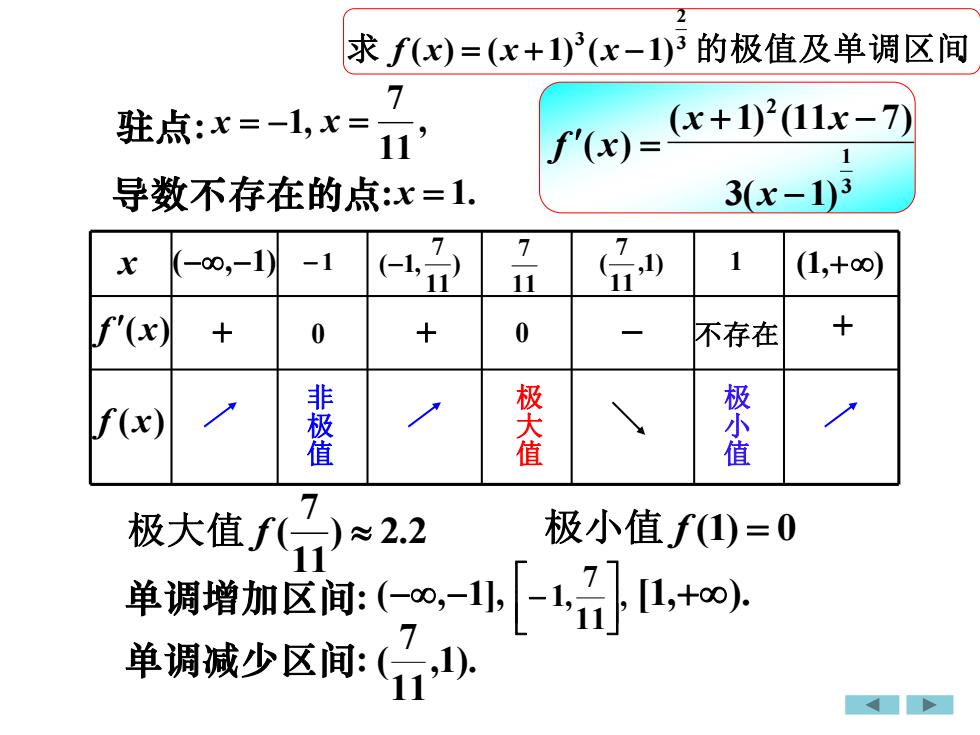
x f (x) f (x) − 1 ) (1,+) 11 7 (−1, 11 7 ,1) 11 7 (−,−1) ( 1 + 0 − 非 极 值 极 小 值 ) 2.2 极小值 f (1) = 0 11 7 极大值 f ( + 0 不存在 + 极 大 值 驻点: x = −1, 导数不存在的点: , 11 7 x = x = 1. ( ) ( 1) ( 1) . 3 2 求 f x = x + 3 x − 的极值及单调区间 f (x) = 3 1 2 3( 1) ( 1) (11 7) − + − x x x 单调增加区间: , [1,+). 11 7 1, (−,−1], − 单调减少区间: ,1). 11 7 (

证对于驻点,有时还可以利用函数在该点寸处的一阶导数的正负号来判断极值点f'(x)- f'(x)f'(x)证 f"(x)= lim<0,linmx→xox-xox-→xo x-Xo因此,当lx一x充分小时,由极限的保号性f'(x)><0.可见,f(x)与x-xo异号.x-xo当x<xo, f'(x) > 0;当x >xo,f'(x)<0.第一充分条件x.处取极大值自己已证极小值情形
定理3(第二充分条件) 证 ( ) 0, 如果 f x0 = 极大值 (极小值). f (x0 ) 0 ( 0),则f (x0 )为 极值的二阶充分条件 f (x0 ) = 0, 0 0 ( ) ( ) lim 0 x x f x f x x x − − → 0 ( ) lim 0 x x f x x x − = → 因此,当 | | x − x0 充分小时,由极限的保号性 0. ( ) 0 − x x f x 可见, f ( x) 与 x − x0 异号. , 当x x0 f (x) 0; , 当x x0 f (x) 0. 所以, ( ) . 第一充分条件 f x 在点x0 处取极大值 对于驻点,有时还可以利用函数在该点 处的二阶导数的正负号来判断极值点. 自己证极小值情形