
如果在点P(xoo)处,自变量x,y咯取增量 △x,△y,函数随之取得增量△z,即 △z=f(xo+△x,yo+△y)-f(xo,yo): 这个增量称为函数zxy)在点P(xo)上的全增量.用 函数的全增量来表述函数在一点处连续的定义记 x=x0+△x,y=y+△y,定义3中的等式 就相当于 lim[f(x,+△x,%+Ay)-f(xo,o】=0, A30 lim△z=0. 即 2012329 Ag根学院信县工程学院高等学教时家

于是与定义3等价的另一个定义是: 定义4设函数zxy)在点P(xoyo)的某一邻域内有定 义,在,点P处的增量为△z,如果 lim△z=0, △x0 △y→0 则称函数zx,)在点Po(xoVo)处连续, 如果函数x,y)在开区域D上各点都连续,则 称函数zx,y)在开区域D上连续.连续的二元函数 ,在几何上表示一张无孔无隙的曲面. 2012329 泰山医学院信息工程学院高等数学教研室 2
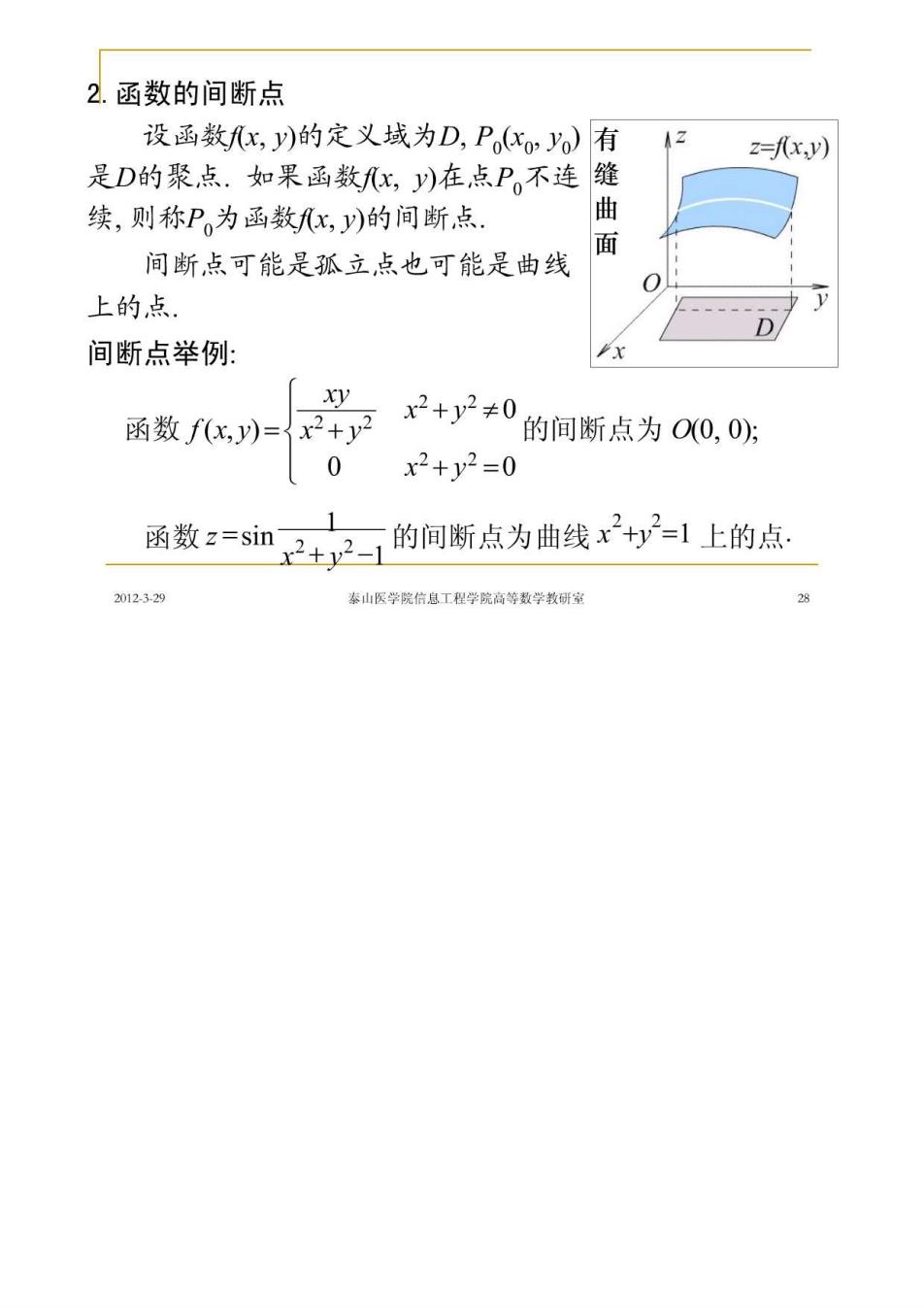
2.函数的间断点 设函数x,y)的定义域为D,Pxo)有 12 2=x,y) 是D的聚点.如果函数x,)在点P不连缝 续,则称P。为函数x,y)的间断点. 曲 间断点可能是孤立点也可能是曲线 面 上的点. 间断点举例: x xy 函数fx,)=x2+y2 x2+y2≠0 的间断点为O0,0: 0 x2+y2=0 函数=s1m2士二的间断点为曲线+1上的点 2012329 泰山医学院信息工程学院高等数学教研室 28

3.二元初等函数: 由变量x,y的基本初等函数及常数经过有限次四 则运算或复合步骤而构成的,且用一数学式子表示的 函数称为二元初等函数, 二元初等函数在其定义区域(是指包含在定义域 内的区域)内是连续。 安禹数m2+了,nF+7了+了 1 3y-2x+5等, 都是二元初等函数,在它们有定义的区域内都是连 n骞的。 泰山医学院信息工程学院高等数学教研室 29

例7.求极限imc+上】 ” 解:f,)中是多元初等函数. y 定义域:D={(,y川x≠0,y≠0.(不连通) 点(1,2)eD1={(x,y)川x>0,y>0}cD. 于是, 站贵-多 y→2 2012329 泰山医学院信息工程学院高等数学教研室