《线性代数》课程教学资源（课件讲稿，C）第二章 2-3向量组的线性关系

第二章矩阵与向量(12)3(-2) 3x, -2x, =12,无解(-2)(633x -2x, = 6

第二章 矩阵与向量 1 2 1 2 3 2 12, 3 2 6. x x x x        3 2 12 3 2 6                     无解

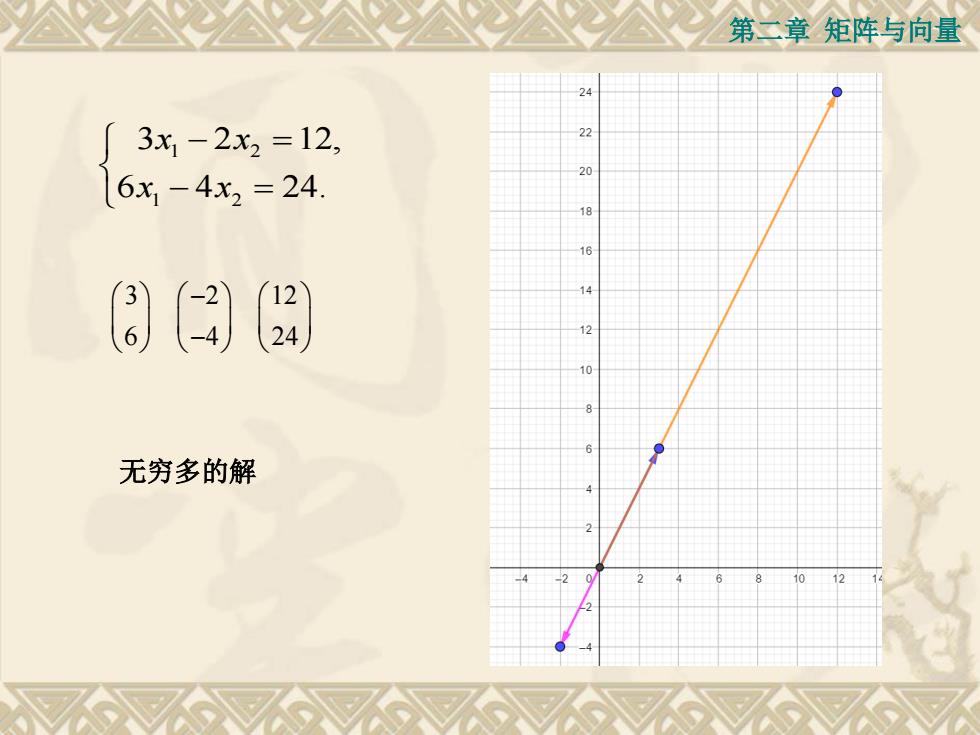
第二章矩阵与向量223x-2x2=12,206x, - 4x2 = 24.1816143(12(-2)12246(-4)108无穷多的解1012

第二章 矩阵与向量 1 2 1 2 3 2 12, 6 4 24. x x x x        3 2 12 6 4 24                     无穷多的解

第二章矩阵与向量一、一个向量与一组向量之间的关系1.线性组合（线性表示）对于向量α,α……,αm和α，若存在m个数1,2,…,m，使得：α= aa + a +...+ Amαm则称α是α1,α2，……,αm的线性组合21,22.,2m称为组合系数或称向量α可由向量组α,α2……αm线性表示显然，零向量是任何一组向量的线性组合

第二章 矩阵与向量 一、一个向量与一组向量之间的关系 1.线性组合（线性表示） 对于向量1 ,2 ,., m和，若存在m 个数1 ,2 ,. ,m ，使得：  = 11 + 22 + .+ mm 则称是1 ,2 ,.,m的线性组合， 1 ,2 ,. ,m 称为组合系数。 显然，零向量是任何一组向量的线性组合 . 或称向量可由向量组1 ,2 ,.,m线性表示

第二章矩阵与向量例1设n维向量81 = (1,0,...,0)8, = (0,1,...,0)8, = (0,0,...,1)α= (a,az,……a,)是任意一个n维向量aα=ae +a,e, +...+ane,所以α是61,62,……,6,的线性组合.通常称1,62,.….,8n为n维单位坐标向量组

第二章 矩阵与向量 1 2 1 2 1 (1,0, ,0) (0,1, ,0) (0,0, ,1) ( , , , ) n n n a a a n             例 设 维向量 是任意一个 维向量 1 1 2 2 1 2 , , , . n n n     a a a        所以 是  的线性组合 通常称 1 2 , , , n     为n维单位坐标向量组

第二章矩阵与向量例2证明向量α=（0,4,2)是α, =(1,2,3), αz =(2,3,1),，α,=(3,1,2)的线性组合，并将α用αj,αz,α,线性表示解：先假定 α=α, αα，即(0, 4, 2) = 2, (1,2,3) + 22(2,3,1) + 2,(3,1, 2)=(2 +22 +32,22 +32 +23,32 +2 +22)因此 +2 +3=0,2 +3 + = 4,32 + 2, +22, = 2

第二章 矩阵与向量 1 2 3 1 2 3 2 (0,4,2) (1,2,3) (2,3,1) (3,1,2) , , .           例 证明向量 是 ， ， 的线性组合， 并将 用 线性表示 1 2 3 (0,4,2) (1,2,3) (2,3,1) (3,1,2)       1 2 3 1 2 3 1 2 3        ( 2 3 ,2 3 ,3 2 )          因此 1 2 3 1 2 3 1 2 3 2 3 0, 2 3 4, 3 2 2.                        解：先假定           1 1 2 2 3 3， 即