《线性代数》课程PPT教学课件（同济第五版）第3章 矩阵的初等变换与线性方程组 3.2 初等矩阵

2、以数k≠0乘某行或某列 以数k≠0乘单位矩阵的第行(×k),得初等 矩阵E(i(k) E(i(k))= ←第i行 上页

2、以数 k  0 乘某行或某列 ( ( )). 0 ( ) E i k k i ri k 矩阵 以数  乘单位矩阵的第 行  ，得初等                       = 1 1 1 1 ( ( ))   E i k k  第 i 行

以Em(i(k)左乘矩阵A, 011 12 E(i(k)A= kop kdin ←第i行 Aml Am2 Amn 相当于以数k乘A的第i行(×k)为 类似地，以E(i(k)右乘矩阵A,其结果 相当于以数k乘A的第i列(C,×k), 区回

相当于以数 k 乘 A的第 i 行 (ri  k)；                 = m m mn i i in n m a a a ka ka ka a a a E i k A          1 2 1 2 1 1 1 2 1 ( ( ))  第 i 行 类似地， 以 Em (i(k))左乘矩阵A， ( ). ( ( )) k A i c k E i k A i n 相当于以数 乘 的第 列  以 右乘 矩阵 ，其结果

3、以数k≠0乘某行（列加到另一行列）上去 以k乘E的第j行加到第i行上(：+g) 或以k乘E的第i列加到第j列上(C;+kc)》 1 1 ←第行 E(ij(k) 1 ←第行 页

3、以数k  0乘某行(列)加到另一行(列)上 去 或以 乘 的第 列加到第 列上 ， 以 乘 的第 行加到第 行上 [ ( ) ( ) j i i j k E i j c kc k E j i r kr + +                       = 1 1 1 1 ( ( ))     k E ij k  第i行  第j行

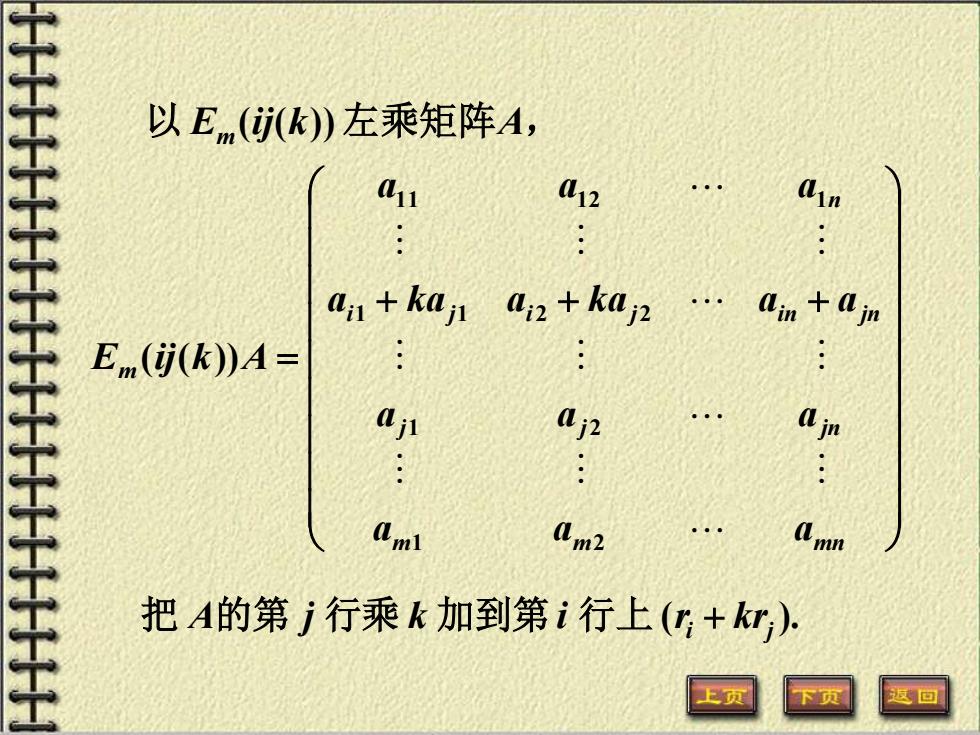
以E,m(jk)左乘矩阵A, 11 L12 an kaj an+kap E(ij(k))A= aj 0j2 把A的第j行乘k加到第i行上(+kr) 区回

以 Em (ij(k))左乘矩阵A，                       + + + = m m m n j j jn i j i j in jn n m a a a a a a a ka a ka a a a a a E ij k A              1 2 1 2 1 1 2 2 1 1 1 2 1 ( ( )) ( ). i j 把 A的第 j 行乘 k 加到第 i 行上 r + kr

类似地，以E,(j(k)右乘矩阵A,其结果相当于 把A的第列乘k加到第j列上(c,+kc), AE,(ii(k avi a,+kay 21 02n am

( ). ( ( )) j i n A i k j c kc E ij k A 把 的第 列乘 加到第 列上 + 类似地，以 右乘矩阵 ，其结果相当于 11 1 1 1 1 21 2 2 2 2 1 ( ( )) n i j i n i j i n m mi mj mi mn AE ij k a a a ka a a a a ka a a a a ka a   +   +   =     +  