《高等数学》课程教学资源（PPT课件）第八章 向量代数与空间解析几何 8-1 第一节 向量及其线性运算

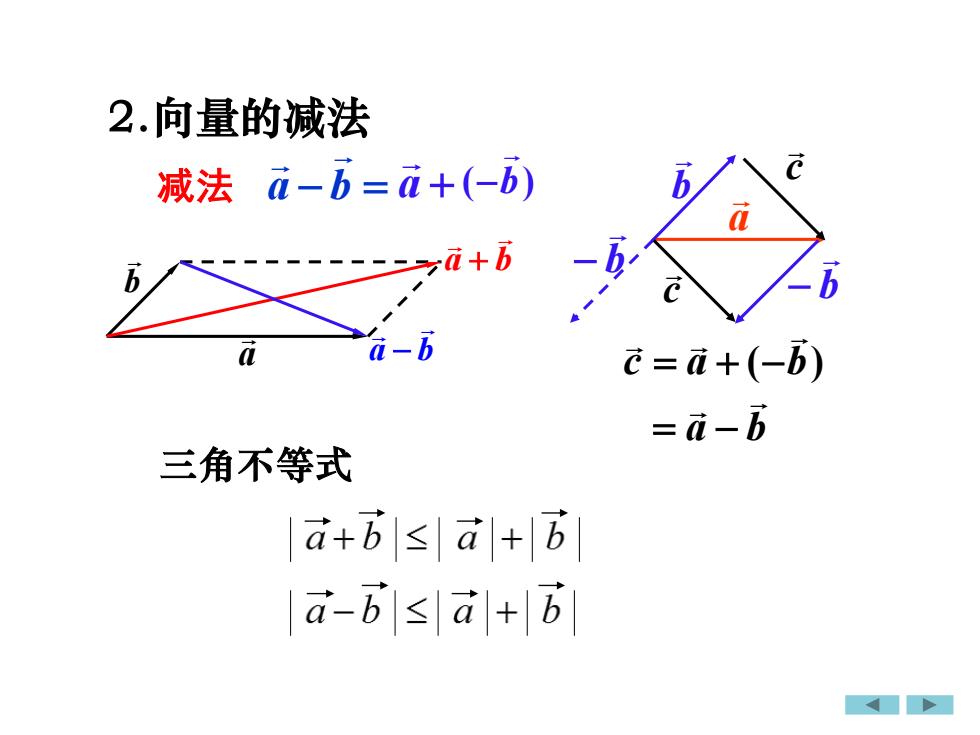
2.向量的减法ca-b=a+(-b)b减法a-b-a+b3ca-bac=a+(-b)=a-b三角不等式a+b|≤|a|+|ba-b|≤|a|+|6

减法 a − b =   a b   b  − b  c −  a b c a b      = − = + (− ) 2.向量的减法 ( b)  a + −  c  a  b  a b   + a b   − 三角不等式

3.向量与数的乘法入是一个数,入与a的乘积是一个新向量，记作a规定>0,a与a同向,alal;= 0, aa = 0;0,a与a反向,a=a总之aa=|a结合律(ua)=u(aa)=aua运算律分配律(a+μ)a=aa+μaa(a+b)=aa+ab

3. 向量与数的乘法  是一个数 , a .   与 a 的乘积是一个新向量, 记作  规定   0, | a | | a |;    =   = 0, 0;   a =   0, | a | | | | a | .    =   a a    与 同向, a a    与 反向, a a   总之  =  运算律 结合律 ( a)    ( a)  =   a  =   分配律 (a b)    + a b   =  + 

定理1.设a为非零向量，则allb b=aa(2为唯一实数)a,,同向时+1设a/b,取=±证“”则b与入同向，且16a|=[6]a=aa故b=aa再证数的唯一性.设又有=μa?,则（-)a=故-=0,，即=

定理1. 设 a 为非零向量 , 则 ( 为唯一实数) 证 “ ” , 取 ＝± 且 再证数  的唯一性 . 则 a∥b 设 a∥b , a , b 同向时 则 b 与  a 同向, 设又有 b＝ a , ( − )a = 0 = = b 故 b a =  . 故   − = 0, 即   =

“一”已知b=a，则当=0时，=0>a//b当a>o时，a,b同向当a<o时，a,b反向例1.设M为ABCD对角线的交点,AB=a,AD=6试用a与b表示 MA,MB,MC,MD解 a+b=AC=2MC =-2MADC66-a= BD=2MD=-2MBMaBMB=-(b-a) A: MA=-(a+b)MC =(a+b)MD=(b-a)

“ ” 则 例1. 设 M 为 M A B 解 D C ABCD 对角线的交点, b a AC = −2MA BD = −2MB 已知 b＝ a , b＝0 a , b 同向 a , b 反向 a∥b a + b = b − a = ( ) 2 1  MA = − a + b ( ) 2 1 MB = − b − a ( ) 2 1 MC = a + b ( ) 2 1 MD = b − a 试用 a 与 b 表示 MA MB MC MD , , , . 当  = 0 时, 当   0 时, 当   0 时

选择题设向量a,砭互相平行，但是方向相反，则当lab>0 时,必有(A)(A)la+b=a|-lbl; (B)la+bal-lbl;(C)la+b<lal-ibl; (D)la+bl=lal+|bl.下列命题是否正确(1)2i>j错向量不能比较大小，只有模才能比较大小，0(2)a ± 0时,,"=1. 错,没有定义向量的除法,a

下列命题是否正确 错 , 错, (1) 2i  j (2)  0 , = 1. a a a     时 选择题 设向量 a b 互相平行,但是方向相反,则当   , | a || b | 0   (A)| a b | | a | | b |;     + = − (D)| a b | | a | | b | .     + = + A 没有定义向量的除法. 向量不能比较大小, 只有模才能比较大小. 时,必有( ) (B)| a b | | a | | b |;     +  − (C)| a b | | a | | b |;     +  −