
例1.讨论p级数1+ 30 h2+.(常数p>0) 的收敛性 解:1)若p≤1,【 因为对一切n∈Z, 1、1 n 而调和级数 发散,由比较审敛法可知p级数 发散
例1. 讨论 p 级数 1 1 1 1 2 3 p p p n + + + + + (常数 p > 0) 的收敛性. 解: 1) 若 p 1, 因为对一切 而调和级数 1 1 n n = 由比较审敛法可知 p 级数 1 n 发散 . 发散
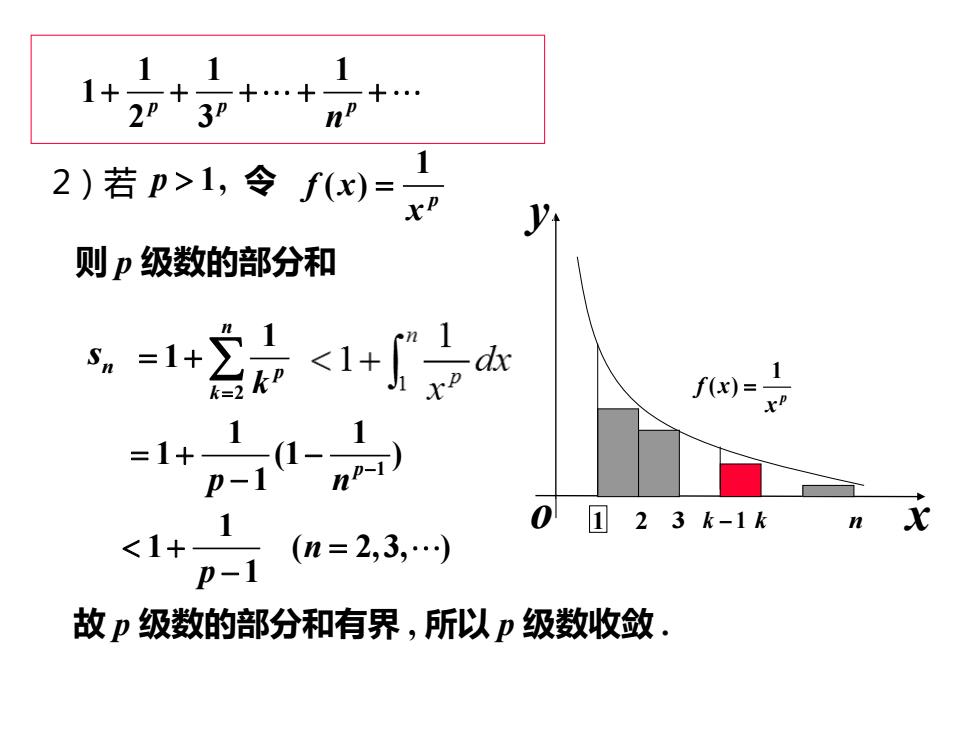
11 1 1+ 2p+30 . 2)若p>1,令f)= y 则p级数的部分和 1 =1+ hP-T 0□23k-1k <1+ p-1 (n=2,3,. 故p级数的部分和有界,所以p级数收敛
p 1, 令 1 1 1 1 (1 ) 1 p p n − = + − − 则 p 级数的部分和 n s 2 1 1 n p k= k = + 故 p 级数的部分和有界 , 所以 p 级数收敛 . 1 1 ( 2,3, ) 1 n p + = − 2)若 1 1 1 1 2 3 p p p n + + + + + 1 ( ) p f x x = 1 n 1 ( ) p f x x = 2 3 k − 1 k x y o

调和级数与p级数是两个常用的比较级数 若存在N∈Z+,对一切n≥W, ()4≥则24n发散: n=l ②(>.则上%收数 n=1 O©O⊙⑨⑧
调和级数与 p 级数是两个常用的比较级数. 若存在 , + N Z 对一切 n N , 机动 目录 上页 下页 返回 结束

例2.证明级数 ∑ √n(n+) 发散 1 证:因为 n(n+1) Vn+1)2 n+1 (n=1,2,.) 而级数 发散 k=2 根据比较审敛法可知,所给级数发散 1 例3.判断级数∑ 的敛散性 台n(n+1)(n+2) 解:因为 ma+2月 的领数收数 根据比较审敛法可知,所给级数收敛 OOo⊙@⑧
证明级数 发散 . 证: 因为 2 ( 1) 1 ( 1) 1 + n n + n 而级数 = = 2 1 k k 发散 根据比较审敛法可知, 所给级数发散 . 例2. 机动 目录 上页 下页 返回 结束 例3. 判断级数 的敛散性 . 解: 因为 3 1 ( 1)( 2) 1 n n n n + + 根据比较审敛法可知, 所给级数收敛

例4.若级数∑an与∑bn均收敛,且an≤cn≤bn n=1 n=1 (n=1,2,),证明级数∑cn收敛 n=1 证::0≤cn-an≤bm-an(n=1,2,),则由题设 ∑(bn-an)收敛>∑(cn-an)收敛 n=l n=1 >∑cn=∑I(cn-an)+an] n=l n=1 00 00 =∑(cn-an)+∑an收敛 n=1 n=l O©O⊙①⑧
例4. 若级数 均收敛 , 且 证明级数 收敛 . 证: n n n n 0 c − a b − a (n = 1 , 2 , ), 则由题设 ( ) 1 n n n b − a = 收敛 ( ) 1 n n n c − a = 收敛 [( ) ] 1 n n n n = c − a + a = ( ) 1 n n n = c − a = = + n 1 n a 收敛 机动 目录 上页 下页 返回 结束