
第七节 第十一章 停里叶级款 一、 三角级数及三角函数系的正交性 二、 函数展开成傅里叶级数 三、 正弦级数和余弦级数
第七节 一、三角级数及三角函数系的正交性 机动 目录 上页 下页 返回 结束 二、函数展开成傅里叶级数 三、正弦级数和余弦级数 第十一章 傅里叶级数
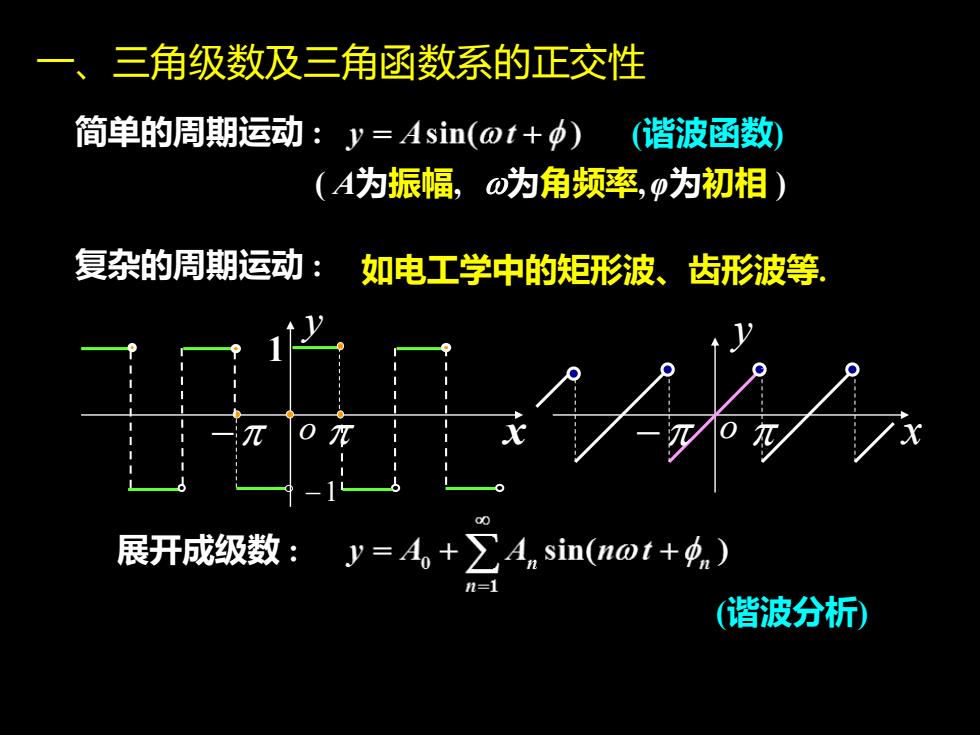
、 三角级数及三角函数系的正交性 简单的周期运动:y=Asin(ot+p) (谐波函数) (A为振幅,o为角频率,p为初相) 复杂的周期运动:如电工学中的矩形波、齿形波等 展开成级数: y=A+∑A sin(m@t+9 (谐波分析)
一、三角级数及三角函数系的正交性 简单的周期运动 : (谐波函数) ( A为振幅, 复杂的周期运动 : 为角频率,φ为初相 ) (谐波分析) 如电工学中的矩形波、齿形波等. 展开成级数 : o y x −1 − 1 − y o x

Jy=A,+∑4nsin(nt+) A+A sin cos not+A,cosg sinnot 得函数项级数 + ∑(a,cOS+b,sinnx)) 称为三角级数, 2 n=1 问题:如何将函数展开成三角级数(傅里叶级数)?
0 A A n t A n t + + n n n n sin cos cos sin 令 , n a , n b 得函数项级数 0 1 ( cos sin ) 2 n n n a a nx b nx = + + 称为三角级数. 问题: 如何将函数展开成三角级数(傅里叶级数)?

定理1.组成三角级数的函数系 1,cosx,sinx,cos2x,sin2x,.,cosx,sinnx,. 在[-π,π]上积分正交,即其中任意两个不同的函数之积在 [-π,π]上的积分等于0. 证:1-cosdx=∫1 sind=0(n=l,2, rπ cos kx cosnxdx coskxcosnx =[cos(k+n)x+cos(k-n)x -[osk+mx+cosk-mr]Hx=0(k≠列 同理可证:2 sinsin=0(k≠n) coskxsind=0 机动 上页下页返回结球
cos(k n)x cos(k n)x d x 2 1 = + + − − 定理 1. 组成三角级数的函数系 证: − 1 cos nxd x = − 1 sin nxd x = 0 cos kx cos nxdx − = 0 sin sin d = 0 − kx nx x 同理可证 : 积分正交 , 上的积分等于 0 . 即其中任意两个不同的函数之积在 cos sin d = 0 − kx nx x (k n ) 机动 目录 上页 下页 返回 结束

但是在三角函数系中两个相同的函数的乘积在[一π,π] 上的积分不等于0.且有 [1-1dx=2元 cosnx dx=π (n=1,2,.) sin2nxdx=元 cos2 nx= 1+cos2nx sin2 nx= 1-cos 2nx 2 2 8 汉▣ 结
上的积分不等于 0 . 11d = 2 − x sin nxdx 2 − cos n xdx 2 − , 2 1 cos 2 cos2 nx nx + = 2 1 cos 2 sin2 nx nx − = 且有 = = 但是在三角函数系中两个相同的函数的乘积在 机动 目录 上页 下页 返回 结束