《高等数学》课程教学资源（PPT课件）Ⅱ_第九章 第七节 方向导数与梯度

第八章第七节方向导数与梯度方向导数梯度-三、物理意义机动自录上页下页返回结束

第八章 第七节 一、方向导数 机动 目录 上页 下页 返回 结束 二、梯度 三、物理意义 方向导数与梯度

一、方向导数设l是xoy平面上以点P(xo,yo)为始点的一条射线，é,=(cosα,cosβ)是与l同方向的单位向量x=xo+tcosα射线l的参数方程为(t ≥ 0)(y= yo + tcosβ设函数z = f(x,y)在点 Po(xo,yo)P(x,y)e的某一邻域U(P)内有定义,P(xo + tcosα, yo + tcos β) 为 l上P(xo, yo)另一点，且PU(Po)x考虑lim[PP][PP/->0

o • 0 0 0 P x y ( , ) l e y x • P x y ( , ) 一、方向导数 0 0 0 0 0 0 0 ( , ) ( , ) ( ) ( cos , cos ) ( ) = + +  设函数 在点 的某一邻域 内有定义， 为 上 另一点，且 ． z f x y P x y U P P x t y t l P U P   l 0 0 0 ( , ) (cos ,cos ) 设 是 平面上以点 为始点的一条 射线， 是与 同方向的单位向量. l l xoy P x y e l =   射线l 的参数方程为  0 0 cos ( 0). cos x x t t y y t   = +  = + 0 0 0 考虑 lim . PP z → PP 

z = f(xo + tcosα, yo +tcos β)- f(xo,yo), PPo= t定义函数z=f(x,y)的增量△z与P到P两点间的距离PP=t之比值，当P沿着l趋于P（即t→0+)时,如果此比的极限存在，则称这极限为函数在点P沿方向l的方向导数.记为P(x,y)0zaf或[(Xo,yo)[(xo,yo)alalPo(xo,yo)afAzAz即lim= limX[(xo,yo)PPCal[PP|→>0*t->0+f(xo + tcosα,yo +tcos β)- f(xo,yo)= limt->0

记为 0 0 0 0 ( , ) 0 函数 的增量 与 到 两点间的距离 之比值, 当 沿着 趋于 (即 )时, 如果 此比的极限存在, 则称这极限为 定义 函数在点 沿方向 的方向导数． z f x y z P P PP t P l P P l t + =  = → 0 0 0 ( , ) 0 0 0 0 0 0 0 0 lim lim ( cos , cos ) ( , ) lim + + + → → → = = + + − =     即 x P t y P t f z z t f x t y t t P x l f y P   0 0 0 0 ( , ) ( , ) . x y x y z f l l     或 0 0 0 0  = + + − z f x t y t f x y ( cos , cos ) ( , ),   PP t 0 = o y x • P x y ( , ) • 0 0 0 P x y ( , ) l t

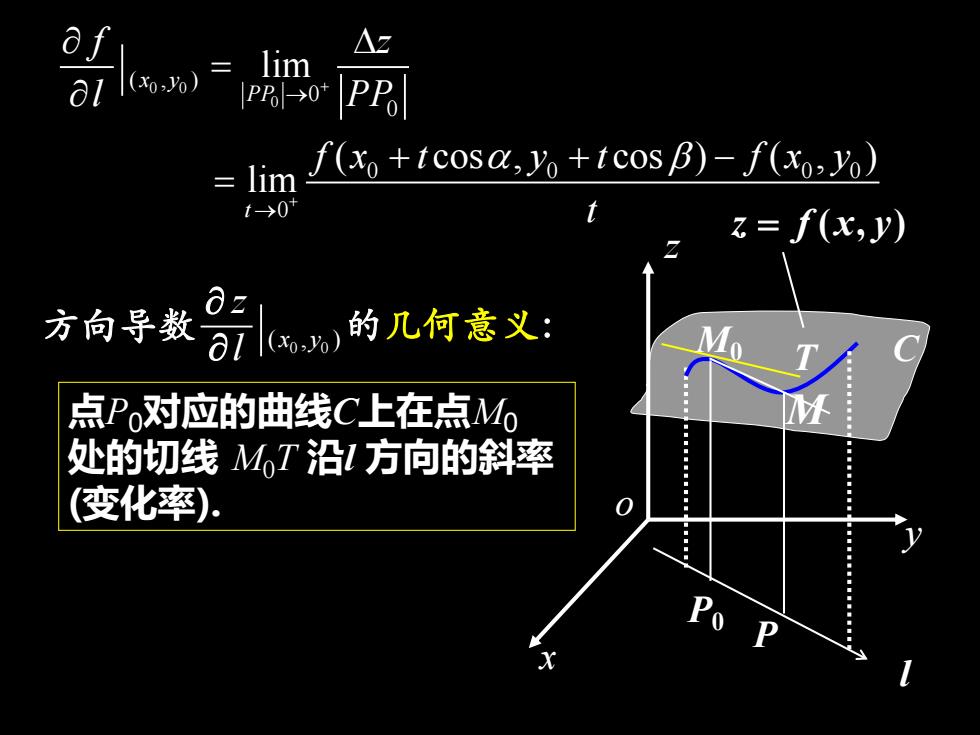
afAzlim1(xo.y0al[PP/->0f(x +tcosα,yo + tcos β) - f(xo,yo)limt→0z = f(x,y)a方向导数的几何意义：al(xo,yo)点Po对应的曲线C上在点MoM处的切线MT沿I方向的斜率(变化率)。0

点P0对应的曲线C上在点M0 处的切线 M0T 沿l 方向的斜率 (变化率). l C P0 T M0 M P o x z y 0 0 ( , ) x y z l 方向导数 的几何意义：   0 0 0 0 0 0 0 0 0 ( , ) 0 lim ( cos , cos ) ( , ) lim + + → →   = + + − =  t x y PP f x t y t f x f z l P y t P   z f x y = ( , )

az注：(1)方向导数就是函数z=f(x,y)[(xo,y0)al在点Po(xo,yo)沿方向1 的变化率。az(2)若偏导数(0,%)存在，取=7 =(1,0),axazaz则存在且等于[(0,%）；反之不然[(xo,yo)axalaz(3) 若偏导数存在，取éj=j=(O,1)(xo.yo)ay0zaz则存在且等于[(xo%)；反之不然I(xo,yo) ayal如z= /x?+ y2在(0,0)点

0 0 ( , ) 0 0 0 (1) ( , ) ( , ) x y z z f x y l P x y l 注： 方向 就是函数 在点 沿方向 数 化 . 导 的变 率  =  0 0 ( , ) (2) 若偏导数 x y 存在，取 l (1,0)， z x e i = =   0 0 0 0 ( , ) ( , ) ; x y x y z l z x 则 存在且等于     反之不然. 0 0 ( , ) 若偏导数 x y 存在，取 el (0,1) ， z j y =  =  0 0 0 0 ( , ) ( , ) ; x y x y z l z y 则 存在且等于     反之不然. 2 2 如 z x y = + 在(0,0) . 点 (3)