
01微分的概念OOOORA人邮教育定理2.6函数y=f(x)在xo处可微Uf(x)在xo处可导,且dy=fdxo)Dx.证:“必要性”已知=f(x)在点x可微,Dy= f(x +Dx)- f(x) = ADx +o(DxDyo(Dx)= lim(A+lim=ADrRoDxDxDrRO故 =f(x)在点xo的可导,且fdx)=A
6 函数 在 处可微 在 处可导,且 定理2.6 01 微分的概念 证: “必要性” 已知 在点 可微 , 故 在点 的可导, 且
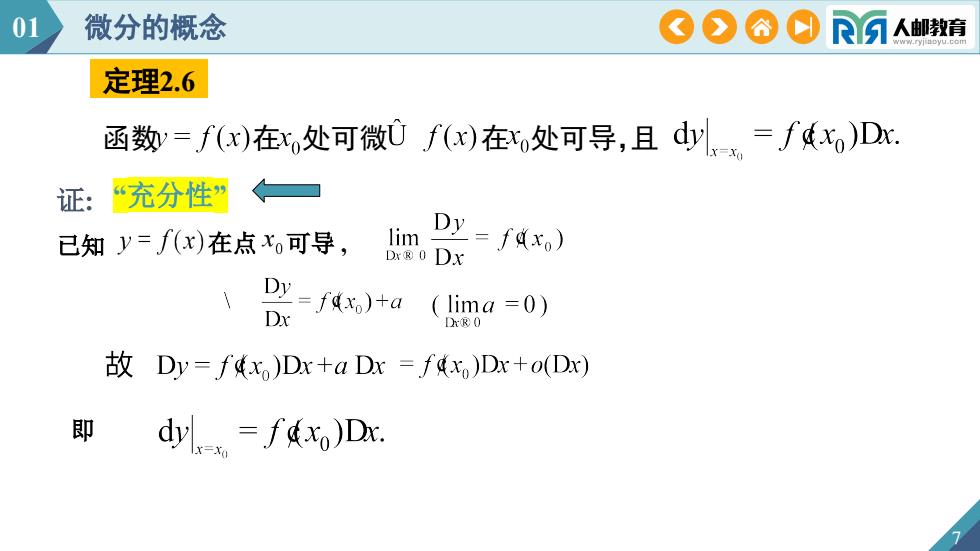
01微分的概念OOOOR人邮教育定理2.6函数y=f(x)在xo处可微Uf(x)在xo处可导,且dy=fdxo)Dx.“充分性”证:Dy=fdxo)lim已知y=f(x)在点x。可导,DrRODXDy=fdxo)+a(lima =0)DxDr?0故 Dy= fdxo)Dx+a Dx = fdxo)Dx+o(Dx)即 dyr = f dxo)Dx
7 函数 在 处可微 在 处可导,且 定理2.6 01 微分的概念 证: 已知 在点 可导 , 即 “充分性

01微分的概念COAOR人邮教育注:记作dy=fdx)Dx函数在点x。的微分,1.规定dx=Dx,则dy=fdxo)dx2.函数在任意点x的微分,记作dy=fdx)Dx=fdx)dx
8 函数在点 的微分, 记作 1.规定 ,则 2.函数在任意点x的微分, 注: 记作 01 微分的概念

01微分的概念COA0R人邮教育例求函数V=x在x=2处的微分解由y=3x2,当x=2时,Ody lx=2=3×22dx =12dx
9 . 解 例 1 由 ,当 x = 2时, 求函数 01 微分的概念 在 x = 2 处的微分
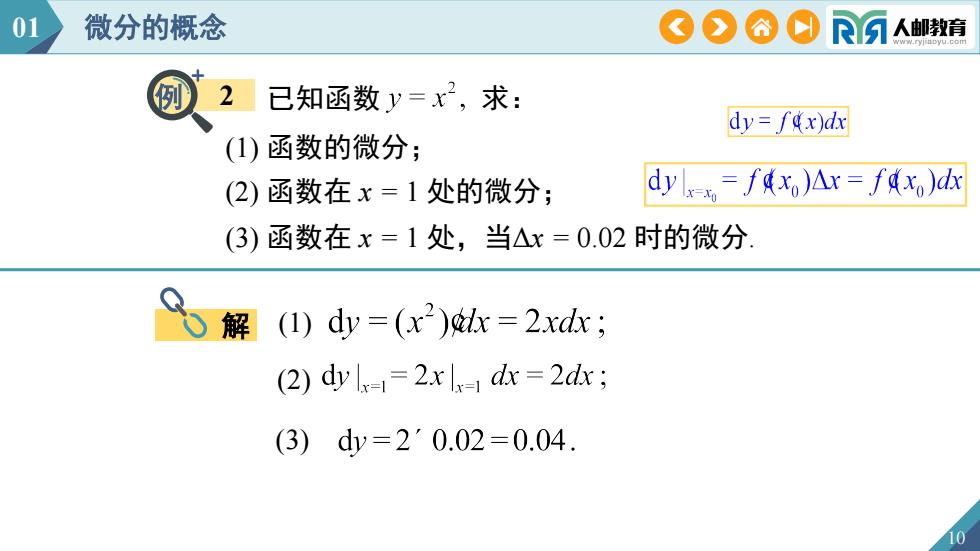
01微分的概念OOAO人邮教育例2已知函数=x2,求:dy= fdx)dx(1)函数的微分;dylx-= fdx)Ax = fdxo)dx(2)函数在x=1处的微分;(3)函数在x=1处,当△x=0.02时的微分(1) dy =(x2)dx = 2xdx ;心解(2) dy |x=I= 2x x= dx = 2dx ;(3)dy=2' 0.02=0.04
10 解 例 2 01 微分的概念 已知函数 求: (1) 函数的微分; (2) 函数在 x = 1 处的微分; (3) 函数在 x = 1 处,当Δx = 0.02 时的微分. (1) (2) (3)