
目录同济大学高等数学试卷选编325(一)高等数学(下)期中考试试卷(「)325试题326参考答案329(二)高等数学(下)期中考试试卷(Ⅱ)329试题330参考答案332(三)高等数学(下)期末考试试卷(「)332试题333参考答案336(四)高等数学(下)期末考试试卷(Ⅱ)336试题337参考答案

一、《高等数学》(第七版)下册习题全解

第八章向量代数与空间解析几何习题8向量及其线性运算1.设u=a-b+2c.v=-a+3b-c.试用a.b.c表示2u-3v解2u-3v=2(a-b+2c)-3(-a+3b-c)=5a-11b+7c2.如果平面上一个四边形的对角线互相平分,试用向量证明它是平行四边形证如图8-1,设四边形ABCD中AC与BD交于点M,已知AM=MCDM=MB故AB=AM+MB-MC+DM=DC即AB/DC且|ABL=|DC|因此四边形ABCD是平行四边形DBDDDCDr图8-2图8-13.把△ABC的BC边五等分,设分点依次为D,Dz,D3D4,再把各分点与点A连接试以AB=C.BC=a表示向量DA,DA,DA和DA证如图8-2,根据题意知BD,-a,D,D-fa,D,D-号Ta,D,D =fa6故1DA=-(AB+BD)=a1-52DA=-(AB+BD,)=53D,A=-(AB+BD)=-5a~c

4一、《高等数学》(第七版)下册习题全解DA- -(AB+BD:)=-4a"sa-c.4.已知两点M,(0,1,2)和M2(1,-1,0).试用坐标表示式表示向量M,M,及-2M,M,解M,M,=(1-0,-1-1,0-2)=(1-2,-2).-2MM,=-2(1,-2. -2)=(-2.4.4)5.求平行于向量a=(6.7,-6)的单位向量4解向量a的单位向量为一,故平行于向量a的单位向量为a67-6六(6,7,-6)= ±(Ta=+((u其中|a/=/62+72+(-6)2=116.在空间直角坐标系中,指出下列各点在哪个卦限?A(1.-2,3),B(2.3.-4).C(2.-3,-4).D(-2.-3.1)解A点在第四卦限,B点在第五卦限,C点在第八卦限,D点在第三卦限,7.在坐标面上和在坐标轴上的点的坐标各有什么特征?指出下列各点的位置A(3.4.0).B(0.4.3).C(3.0.0).D(0,-1.0).解在坐标面上的点的坐标,其特征是表示坐标的三个有序数中至少有一个为零.比如x0y面上的点的坐标为(xo,yo,0),x0z面上的点的坐标为(xo.0.0).y0:面上的点的坐标为(0,yo,z0).在坐标轴上的点的坐标,其特征是表示坐标的三个有序数中至少有两个为零比如x轴上的点的坐标为(xo.0.0),y轴上的点的坐标为(0.10.0),2轴上点的坐标为(0,0,z0)A点在xOy面上,B点在yOz面上,C点在x轴上,D点在y轴上8.求点(a,6b,c)关于(1)各坐标面:(2)各坐标轴:(3)坐标原点的对称点的坐标.解(1)点(a,b,c)关于xOy面的对称点为(a,b,-c),关于y0z面的对称点是(-a,b,c),关于z0x面的对称点为(a,-b.c)(2)点(a,b,c)关于x轴的对称点是(a,-b,-c)关于轴的对称点是(-a.b,-c),关于z轴的对称点是(-a,b.c)(3)点(a,b,e)关于坐标原点的对称点是(-a,-b,-c).9.自点P。(xo,yo,zo)分别作各坐标面和各坐标轴的垂线,写出各垂足的坐标解设空间直角坐标系如图8-3.根据题意,PF为点P关于0面的垂线,垂足F坐标为(x0.0.z0):P.D为点P.关于xO面的垂线,垂足D坐标为(10.0.0):PE为点P。关于yO面的垂线,垂足E坐标为(0.o.)PoA为点P.关于x轴的垂线,重足A的坐标为(o.0.0):PB为点P.美于轴
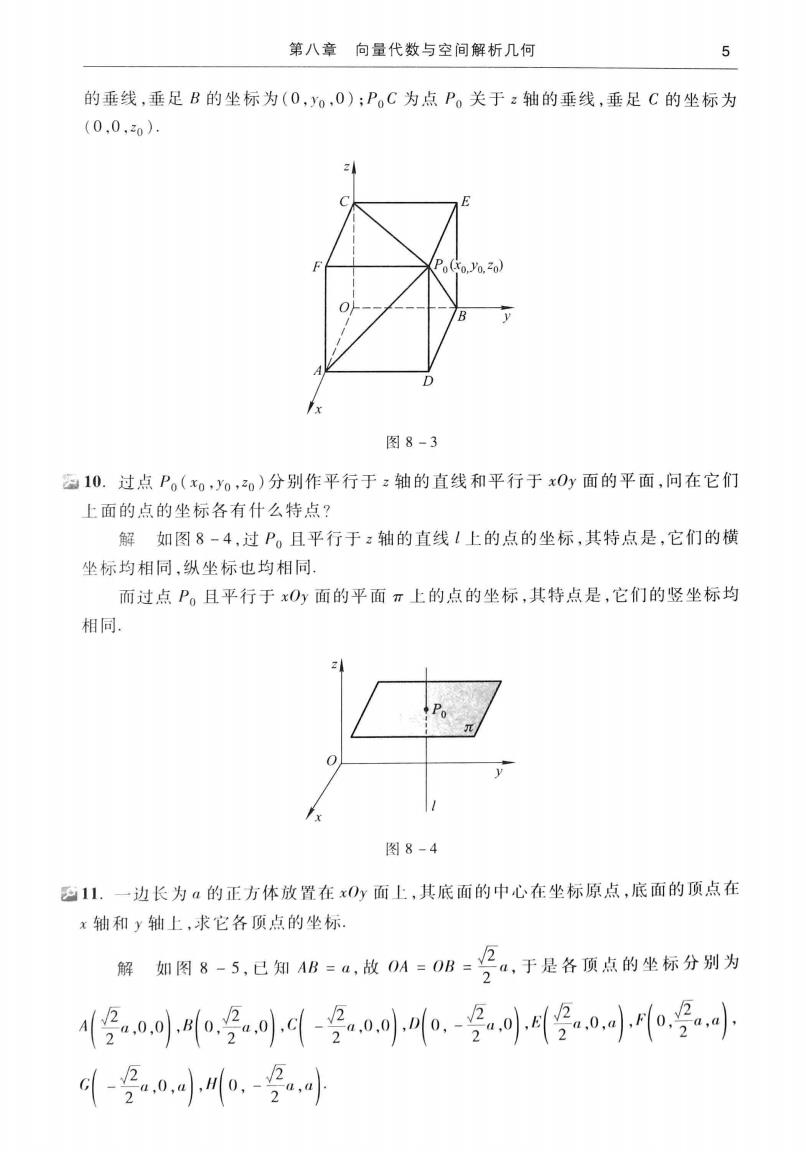
第八章向量代数与空间解析几何5的垂线,垂足B的坐标为(O,Yo,O);P。C为点Po关于z轴的垂线,垂足C的坐标为(0,0,20).Z0(to,0,20)yfD图8-310.过点Po(xo,yo,zo)分别作平行于z轴的直线和平行于x0y面的平面,问在它们上面的点的坐标各有什么特点?解如图8-4,过P。且平行于z轴的直线1上的点的坐标,其特点是,它们的横坐标均相同,纵坐标也均相同而过点P。且平行于xOy面的平面π上的点的坐标,其特点是,它们的竖坐标均相同Z1y图8-411.一边长为a的正方体放置在x0y面上,其底面的中心在坐标原点,底面的顶点在x轴和轴上,求它各顶点的坐标.J2,于是各顶点的坐标分别为如图8-5,已知AB=a,故OA=OB=解2..)(.).2a.0.0) 0(0. Pa.0.) (.-a.0) c(/2a.0)以222a."a2