
第二章矩阵与向量 例如,一般元线性方程组 411X1+012X2+.+41nXn=b1 L21七1+422X2+.+42mXn=b2 (8) amx+am2x2+.+amnxn=bm 的未知量的系数可以用矩阵A=(a,)mxm 来表示, 此时称A为方程组的系数矩阵
第二章 矩阵与向量 例如,一般n元线性方程组 此时称A为方程组的系数矩阵. ( ) 的未知量的系数可以用矩阵 A a = ij m n 来表示, 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 . . (8) . . n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b + + + = + + + = + + + =
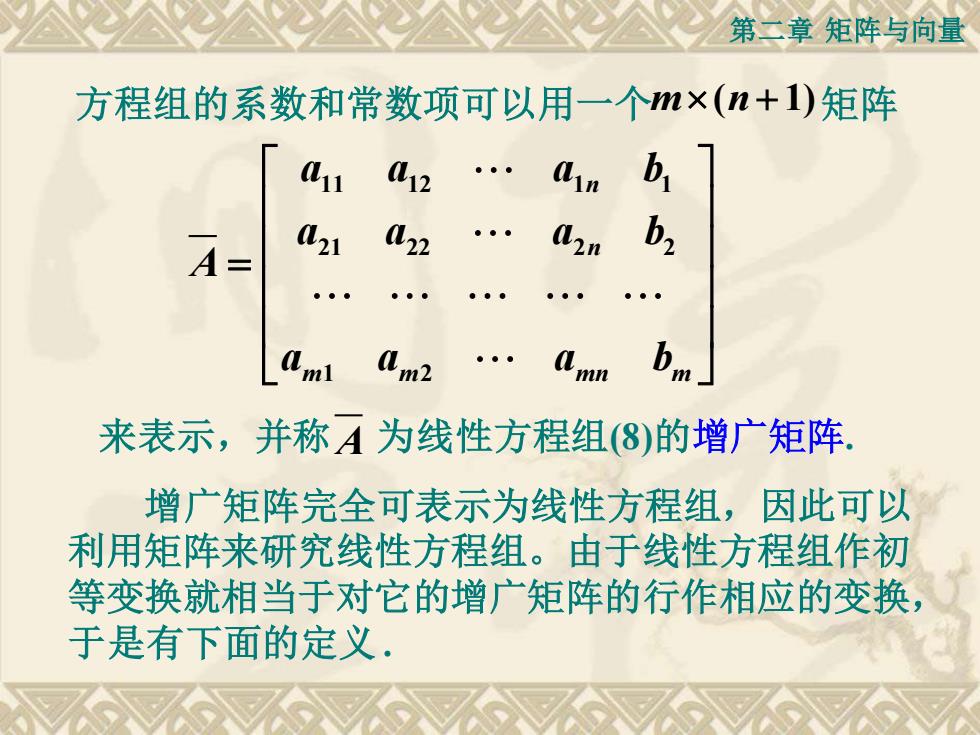
第二章矩阵与向量 方程组的系数和常数项可以用一个m×(n+1)矩阵 1 12 b A= L21 22 b, Am2 来表示,并称A为线性方程组(⑧)的增广矩阵 增广矩阵完全可表示为线性方程组,因此可以 利用矩阵来研究线性方程组。由于线性方程组作初 等变换就相当于对它的增广矩阵的行作相应的变换, 于是有下面的定义
第二章 矩阵与向量 来表示,并称 A 为线性方程组(8)的增广矩阵. 11 12 1 1 21 22 2 2 1 2 n n m m mn m a a a b a a a b A a a a b = 增广矩阵完全可表示为线性方程组,因此可以 利用矩阵来研究线性方程组。由于线性方程组作初 等变换就相当于对它的增广矩阵的行作相应的变换, 于是有下面的定义 . 方程组的系数和常数项可以用一个 m n + ( 1) 矩阵