
说明:△y=f'(xo)△x+o(△x) dy=f'(xo)△x 当f'(x)≠0时, lim △y=lim △y △x→0dy △r-→0f'(x0)△x 1 lim Ay =1 f(xo)Ax0 Ax 所以△x→0时△y与dy是等价无穷小,故当△x 很小时,有近似公式 △y≈dy 2009年7月3日星期五 6 目录 上页 下页 、返回
2009年7月3日星期五 6 目录 上页 下页 返回 0 f x ′()0 ≠ 时 , y = f ′ )(d Δxx0 )()( 0 y =Δ f ′ Δ + Δxoxx y y x d lim0 Δ →Δ xxf y x ′ Δ Δ = →Δ )( lim 0 0 x y xf x Δ Δ ′ = →Δ 0 0 lim )( 1 = 1 所以 Δx → 0 时 Δ y dy 很小时, 有近似公式 Δ x Δy y ≈ d 与 是等价无穷小, 当 故当 说明 :
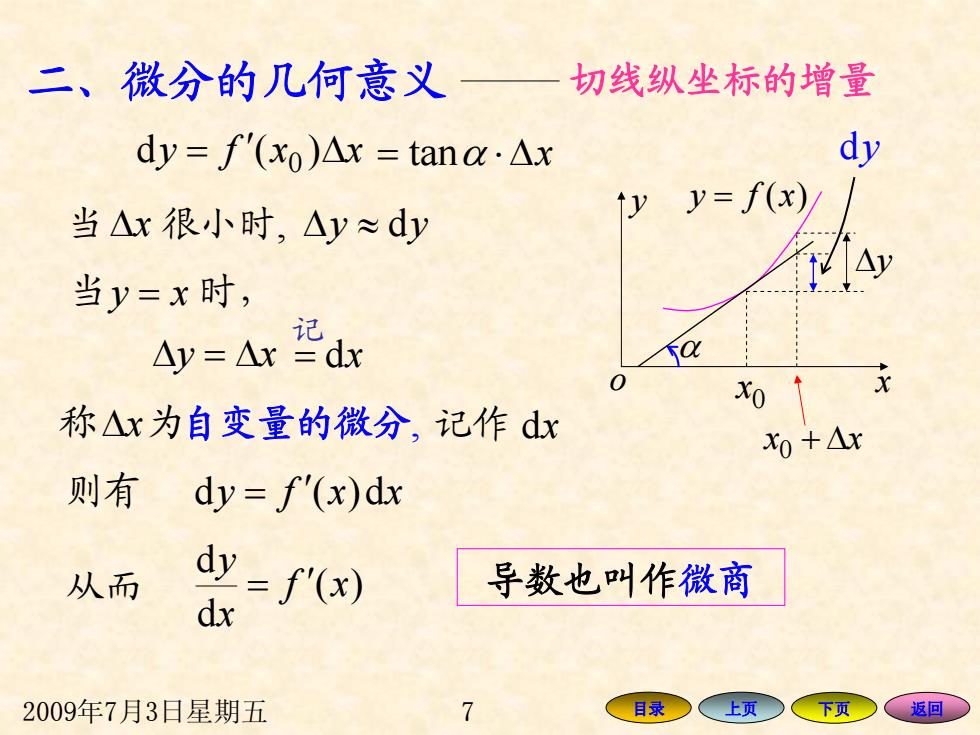
二、微分的几何意义 切线纵坐标的增量 dy=f'(xo)△x=tana:△x dy 当△x很小时,△y≈dy ↑yy=f(x)/ 当y=x时, Ay=Ax dx 称△x为自变量的微分,记作dx 0+△x 则有 dy=f(x)dx 从而 =f(x) 导数也叫作微商 dx 2009年7月3日星期五 7 目录 上页 下页 、返回
2009年7月3日星期五 7 目录 上页 下页 返回 二、微分的几何意义 切线纵坐标的增量 y = f ′ x )(d Δx 0 + Δxx0 x y o = xfy )( α 0 x Δy = tan α ⋅Δ x dy 当 很小时 Δx , Δy ≈ dy 当 = xy 时, 则有 dy = f ′ x)( dx 从而 )( d d xf x y = ′ 导数也叫作微商 称 Δx 为自变量的微分, 记作 dx Δy Δ= x = dx 记