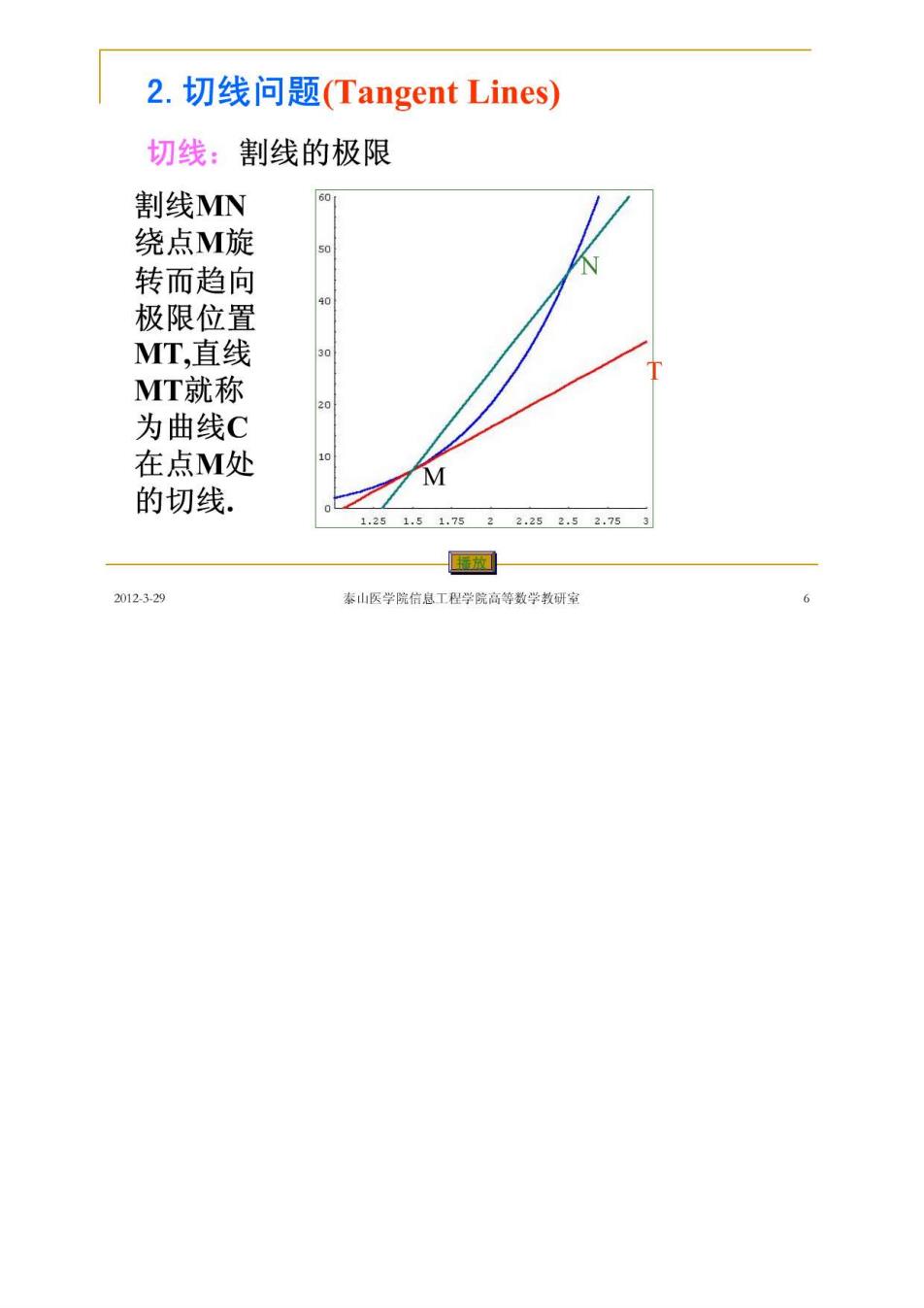
2.切线问题(Tangent Lines) 切线:割线的极限 割线MN 绕点M旋 转而趋向 极限位置 MT,直线 MT就称 为曲线C 在点M处 M 的切线. 1.251.51.7522252.52753 网 2012329 泰山医学院信息工程学院高等数学教研家

设M(xo,yo),N(x,y). y=f(x)入 割线MN的斜率为 2 C M tano=-o x-xo -(x)-) Xo x-x。 N沿曲线CM,x→x0, 切线MT的斜率为k=tana=lim f(x)-f(xo) x→x0X-X0 2012329 泰山医学院行息工程学院高等数学教研室

二导数的定义 (Definition of Derivatives) 1.定义设函数y=f(x)在点x的某个邻域内 有定义,当自变量x在x处取得增量△x(点 x,+△x仍在该邻域内)时,相应地函数y取 得增量△y=f(x,+△x)-f(x);如果△y与 △x之比当△x→0时的极限存在,则称函数 y=f(x)在点x处可导,并称这个极限为函 数y=f(x)在点x处的导数,记为yx=, 的1 在f'(x) 2012329 素山医学院信息工程学院高等数学教研室

即y=l △y=im (x。+△x)-f(x) Ar→0△XAr→0 △x 导数定义其它常见形式: f(xo)=lim f(x)-f(xo) r→xa x-xo f(x)=lim(-f(x.) h 2012329 素山医学院信息工程学院高等数学教研室

注1) △y表示因变量在以x,和x,+△x 为端点的区间上的平均变化率 2)f'(x)是因变量在点x处的变化率,它 反映了因变量随自变量的变化而变化的快 慢程度. 3)如果四是不存在,则称=心在不可导。 若1imAy=o,称y=f(在x,处的导数为无穷大. Ar→0△r 2012329 泰山医学院信息工程学院高等数学教研室 10