
第一章 第二节 数列的版很 一、数列极限的定义 二、收敛数列的性质 三、极限存在准则 Qao⊙@8
第一章 二 、收敛数列的性质 三 、极限存在准则 一、数列极限的定义 第二节 机动 目录 上页 下页 返回 结束 数列的极限
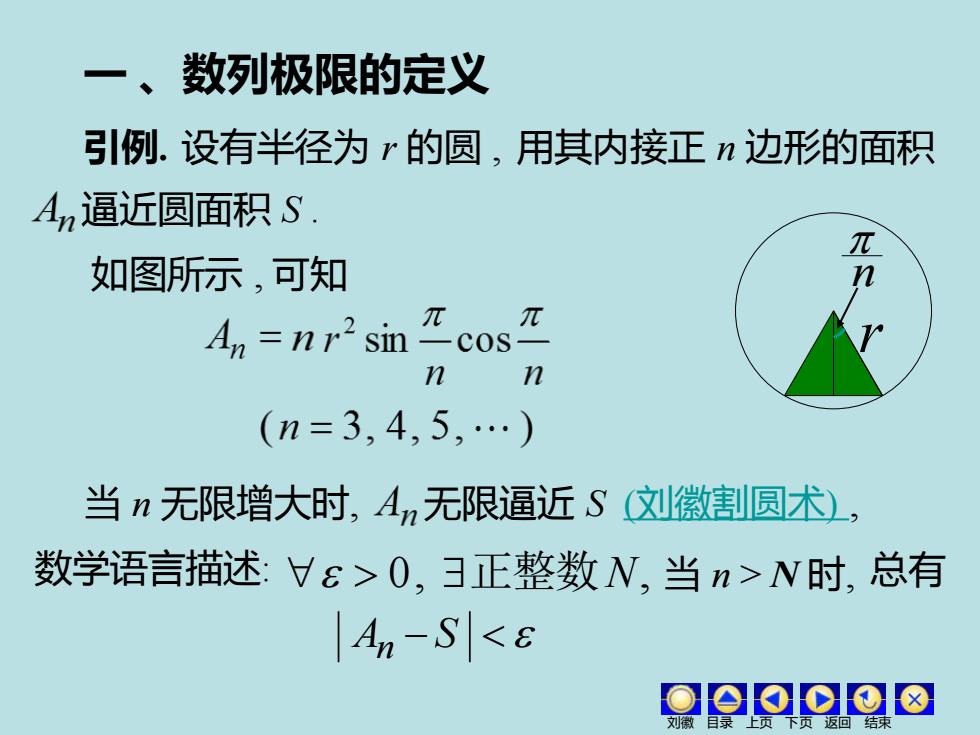
一、数列极限的定义 引例.设有半径为r的圆,用其内接正n边形的面积 An逼近圆面积S. 如图所示,可知 ππ An =nr2 sin "cos n n (n=3,4,5,.) 当n无限增大时,An无限逼近S刘徽割圆术), 数学语言描述:Ve>0,正整数N,当n>N时,总有 An-S<8 OOo⊙⊙8
数学语言描述: r 一 、数列极限的定义 引例. 设有半径为 r 的圆 , 逼近圆面积 S . 如图所示 , 可知 n 当 n 无限增大时, 无限逼近 S (刘徽割圆术) , 0, 正整数N, 当 n > N 时, A − S n 用其内接正 n 边形的面积 总有 刘徽 目录 上页 下页 返回 结束

定义:自变量取正整数的函数称为数列,记作xn-f(n) 或{xn.xn称为通项(一般项) 若数列{xn}及常数a有下列关系 s>0,3正数N,当n>N时,总有xn-a<6 则称该数列{xn}的极限为a,记作 lim n=a或xn→a(n→oo) n-→o 此时也称数列收敛,否则称数列发散 a-8<Xn<a+8 (n>N) 几何解释: 即xn∈U(a,e) ●00 a-EXN+a xN+2 a+E (n>N) ggo⊙▣⑧
定义: 自变量取正整数的函数称为数列, 记作 或 称为通项(一般项) . 若数列 及常数 a 有下列关系 : 当 n > N 时, 总有 记作 此时也称数列收敛 , 否则称数列发散 . 几何解释 : a − a + ( ) a − x a + n (n N ) 即 x (a, ) n (n N ) x a n n = → lim 或 x → a (n → ) n N+1 x N+2 x 则称该数列 的极限为 a , 机动 目录 上页 下页 返回 结束

123 n 例如, 234 n+1 Xn=n →1(n→o) n+1 143 2 n+(-1)n-1 收 2 3’4 n 敛 n+110m-→0) n 2,4,8,.,2”,. xn=2”-→0(n>0) 发 1,-1,1,.,(10+1, 散 xn=(-1)n+ 趋势不定 Ooo⊙o8 机
例如, , 1 , , 4 3 , 3 2 , 2 1 n + n +1 = n n xn →1 (n →) n n x n n 1 ( 1) − + − = →1 (n →) 2 , 4 , 8 , , 2 n , n n x = 2 → (n →) 1 ( 1) + = − n n x 趋势不定 收 敛 发 散 机动 目录 上页 下页 返回 结束

例1.已知x,= +(-l)” 证明数列{xn}的极限为1, n 证:x,-1=n n Vc>0,欲使xn-1<6,即<6,只要n> 因此,取N=1,则当>N时,就有 nt(l"-lss n 故 limx=lim n+(-1)” =1 n→oo n-→0 n Oao⊙⊙8
例1. 已知 证明数列 的极限为1. 证: xn −1 = 1 ( 1) − + − n n n 0 , 欲使 即 只要 1 n 因此 , 取 ], 1 [ N = 则当 n N 时, 就有 − + − 1 ( 1) n n n 故 1 ( 1) lim lim = + − = → → n n x n n n n 机动 目录 上页 下页 返回 结束