
系统的全响应为: r(t)=rz(t)+rzs(t) =3e-2e-2e+t-2t+2 零输入响应 零状态响应 自由响应 强迫响应 =e-2e2r+t-2t+2
r(t) r (t) r (t) Zi ZS 系统的全响应为: 3 2 2 2 2 2 2 e e e t t t t t 2 2 2 2 2 e e t t t t 零输入响应 零状态响应 自由响应 强迫响应
§2-2离散系统的时域分析 §2-2-1离散系统差分方程的建立 Q:已知RL网络,试从微分方程导出差分方程。 根据VL方程,对图示系统列出方程: VR(1)- i(t) VR(t)+vL(t)=f(t) vL(t) 由于a0=Ri),v,0=L dt i(n) 0+是)=f0 dt 0 4T nT
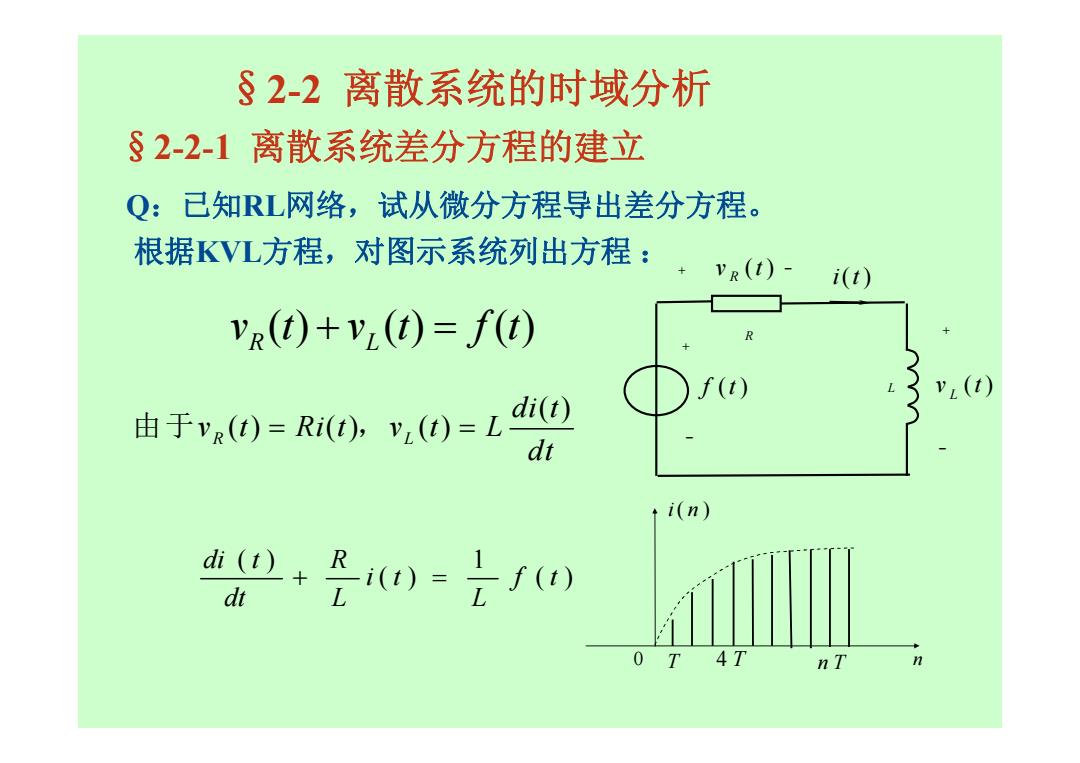
§2-2 离散系统的时域分析 Q:已知RL网络,试从微分方程导出差分方程。 根据KVL方程,对图示系统列出方程 : §2-2-1 离散系统差分方程的建立 v (t) v (t) f (t) R L ( ) ( ) ( ) ( ) R L di t v t Ri t v t L dt 由于 , ( ) 1 ( ) ( ) f t L i t L R dt di t R + – f (t) L v (t) L + – v (t ) R i(t) + – 0 n i n( ) T 4 T n T

对连续变量t,若在t=nT,(n=0,l,2,…)各点取样, 其中T,为取样间隔.则得到激励信号的离散取样序列和 f(nT)输出信号的离散取样序列(nT,)。在足够小的情况 下,微分运算可近似表示为差分运算 di()≈in7,)-i(n-1)T.] dt T 代入原连续 方程得 w)-m-+是,)-2fa,) T、 o-a-+是a=20) 一阶常系数 i(n)- L+RT、 Isfn) 差分方程
对连续变量t,若在 各点取样, 其中 为取样间隔.则得到激励信号的离散取样序列和 输出信号的离散取样序列 。在足够小的情况 下,微分运算可近似表示为差分运算 nTs t (n 0,1,2,) T s ( ) nTs f ( ) nTs i s s s T i nT i n T dt di (t ) ( ) [( 1) ] ( ) 1 ( ) ( ) [( 1) ] s s s s s f nT L i nT L R T i nT i n T 代入原连续 方程得 ( ) 1 ( ) ( ) ( 1) f n L i n L R T i n i n s ( ) ( 1) f (n) L RT T i n L RT L i n s s s 一阶常系数 差分方程

差分方程的阶数=未知序列变量序号的 最大值与最小值之差 后向形式或向右移序的)差分方程: 方程中未知序列的序号是自以递减方式给出。 前向形式(或向左移序的)差分方程: n以递增方式给出,即由y(n)、(n+).y(n+N) 如 y(n+1)+ay(n)=f(n) 此为一阶前向差分方程式 两种描述方法无本质区别,仅仅是延时不同。通常对 因果系统用后向形式的差分方程比较方便,在一般数字滤 波器的描述中多用这种形式。而在状态变量分析中,前向 形式的差分方程较为常用
差分方程的阶数=未知序列变量序号的 最大值与最小值之差 后向形式(或向右移序的)差分方程: 方程中未知序列的序号是自n以递减方式给出。 前向形式(或向左移序的)差分方程: n以递增方式给出,即由 、 、… 如 此为一阶前向差分方程式。 两种描述方法无本质区别,仅仅是延时不同。通常对 因果系统用后向形式的差分方程比较方便,在一般数字滤 波器的描述中多用这种形式。而在状态变量分析中,前向 形式的差分方程较为常用。 y(n) y(n1) y(n N) y(n 1) ay (n) f (n)

§2-2-2离散系统差分方程的求解 迭代法 二经典解法:齐次解十特解 三零输入响应十零状态响应 四 卷积和 五 Z变换 阶常系数线性差分方程的一般形式为: ∑a,y(n-i)=∑bf(n-)
§2-2-2 离散系统差分方程的求解 一 迭代法 二 经典解法:齐次解+特解 三 零输入响应+零状态响应 四 卷积和 五 Z变换 N阶常系数线性差分方程的一般形式为: 0 0 ( ) ( ) N M i l i l a y n i b f n l