
Ch4傅立叶变换在系统分析中的应用 系统的频率响应HG@) frequency response 无失真传输 理想低通滤波器 调制与解调 零阶保持抽样 多路复用
Ch4 傅立叶变换在系统分析中的应用 Application: 滤波、调制、抽样 • 系统的频率响应 H(j) frequency response • 无失真传输 • 理想低通滤波器 •调制与解调 •零阶保持抽样 •多路复用

1频率响应H(j@) H(jo)= Y(j@) F(j0) =FT[h(t)] 2无失真传输 时域上,r(t)=Ke(t-to)》 H(jo)=Ke-jo。=|H(jo)|ejp(o) ↑H(Uo ,↑p(j0) H(jo)=K 0(0)=-0·t0 0 0 0·t0
[ ( )] ( ) ( ) ( ) FT h t F j Y j H j 1 频率响应 H(j) , ( ) ( ) 0 时域上 r t Ke t t 0 ( ) | ( ) | t H j K 2 无失真传输 ( ) ( ) | ( ) | 0 j t j H j Ke H j e H ( j) ( j) 0 t 0 0
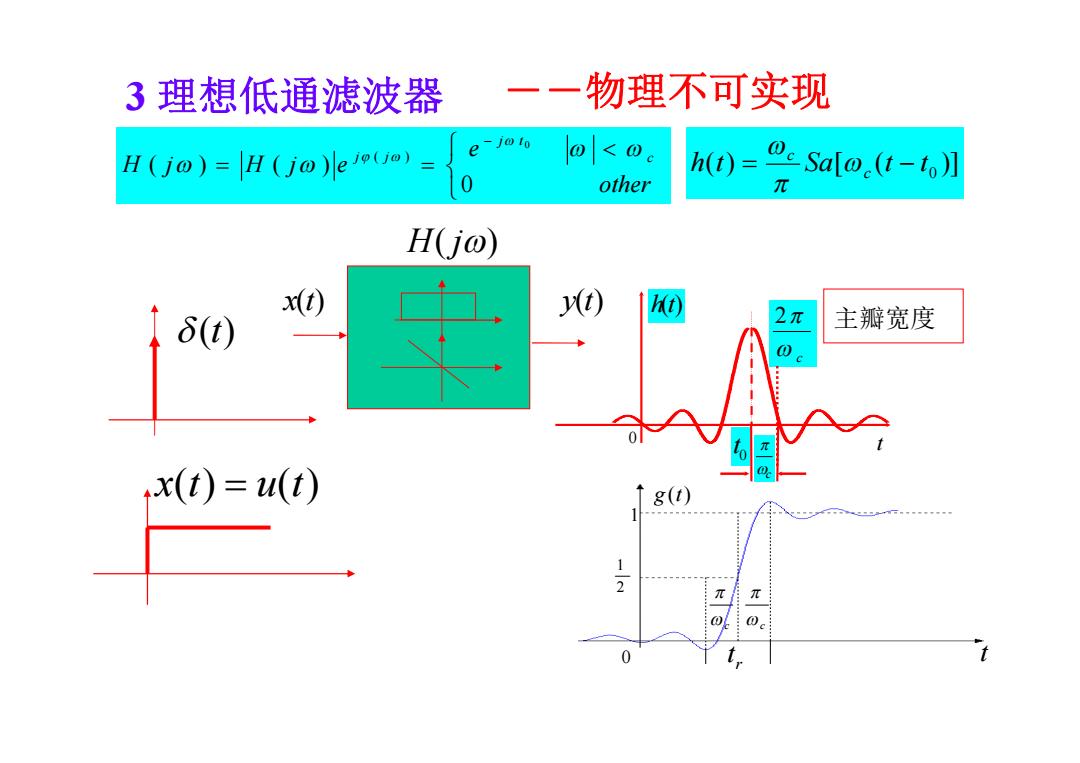
3理想低通滤波器 一一物理不可实现 H(jo)=H(j)e <0 h(t)= Salo.(t-to月 other π H(jo) x(t) y(t) 16(t) 2π 主瓣宽度 0 c +(t)=u(t) 8(t) 2 @c t
H( j) x(t) y(t) 0 t 2 c 主瓣宽度 c h(t) t 0 (t) 1 t g t( ) 0 c c r t 2 1 x(t) u(t) 3 理想低通滤波器 other e H j H j e c j t j j 0 ( ) ( ) 0 ( ) --物理不可实现 ( ) [ ( )] 0 h t Sa t t c c

4物理可实现系统的约束条件 系统物理可实现要求: (1) 时域一因果系统 t<0,h(t)=0 (2) 频域 a.佩利维纳准则: 幅频响应不能在一个频带内为零 b.希尔伯特变换(Hilbert) 因果系统频响的实部和虚部之间相互限制 常见滤波器:1、巴特沃兹(Butterworth) 2、切比雪夫(Chebyshev)
4 物理可实现系统的约束条件 系统物理可实现要求: (1) 时域——因果系统 (2) 频域—— a. 佩利维纳准则: 幅频响应不能在一个频带内为零 b. 希尔伯特变换(Hilbert) 因果系统频响的实部和虚部之间相互限制 t 0, h(t) 0 常见滤波器:1、巴特沃兹(Butterworth) 2、切比雪夫(Chebyshev)

4.7调制与解调 ·调制的目的:发送和传输信号 以某个较高的频率发送信号 在该特定频率的信道中传输 ·调制的手段:进行频谱搬移
4.7 调制与解调 • 调制的目的:发送和传输信号 以某个较高的频率发送信号 在该特定频率的信道中传输 • 调制的手段:进行频谱搬移