华东理工大学：《信号与系统》课程教学资源（试卷习题）各章习题（含解答）

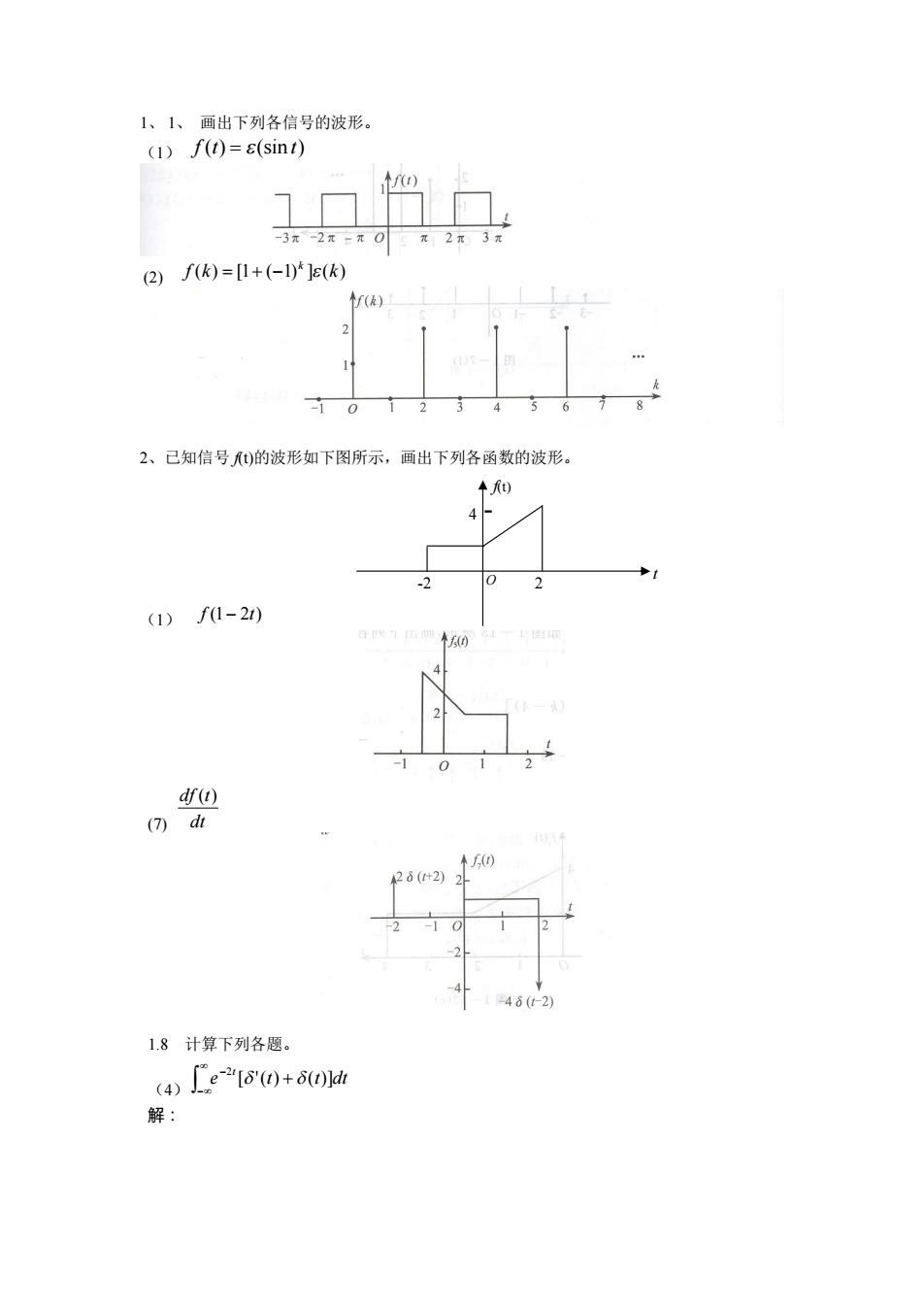
1、1、画出下列各信号的波形。 (1)f(t)=s(sint) 个f) -3π-2π-元0 元2元3元 (2)f)=1+(-1)e() f() 2 10 2、己知信号)的波形如下图所示，画出下列各函数的波形。 十) (1)f1-21) 个0 0 df() (7d 个0 28(+2) -48(12) 1.8计算下列各题。 4e"6)+oh 解：

1、 1、 画出下列各信号的波形。 （1） f (t)   (sin t) (2) f (k) [1 ( 1) ] (k) k     2、已知信号 f(t)的波形如下图所示，画出下列各函数的波形。 （1） f (1 2t) (7) dt df (t) 1.8 计算下列各题。 （4） e t t dt t [ '( ) ( )] 2        解： -2 2 4 t f(t) O

e[6'0+ut =[e6')+e”6t=['0+20+6)t =8'0dh+C360)d=3 r+sm孕5u+2h 解： +sin(+2)d=+sin3 1.18写出下列系统的微分方程或差分方程。 (1) 解：系统框图中含有两个积分器，则该系统是二阶系统。设最下方积分器输出)，则各 积分器的输入为"()，x()。左方加法器的输入为 x"(t)=f(t)-2x(t)-3x'(t) 即'(0)+3x'(0+2x(0=f) 由右方加法器的输出，得 y(t)=x"(t)-2x'(t) 由上式得 y'(t)=[x"()]"-2[x'(t)' 3y'(t)=[3x"(t)]'-2[3x()] 2(t)=[2x"(t]-2[2x'(t)] 将上面三式相加，得 y'()+3y'()+2y) =[x"(t)+3x'(t)+2x(t)]"-2[x"()+3x'(t)+2x(t)] 考虑到f)=x"(0+3x()+2x)上式右端等于"(0-2(0，故得 y"(t)+3y(t)+2y(t0=f"()-2f'() 此即为系统的微分方程。 (2)

                           '( ) 3 ( ) 3 [ '( ) ( )] [ '( ) 2 ( ) ( )] [ '( ) ( )] 2 2 2 t dt t dt e t e t dt t t t dt e t t dt t t t          （5） t dt t t )] ( 2) 4 [ sin( 2        解： )] 3 4 )] ( 2) [ sin( 4 [ sin( 2 2 2         t t t dt t t t    1.18 写出下列系统的微分方程或差分方程。 （1） 解：系统框图中含有两个积分器，则该系统是二阶系统。设最下方积分器输出 x(t) ，则各 积分器的输入为 x' '(t), x'(t) 。左方加法器的输入为 x' '(t)  f (t)  2x(t)  3x'(t) 即 x' '(t)  3x'(t)  2x(t)  f (t) 由右方加法器的输出，得 y(t)  x' '(t)  2x'(t) 由上式得 2 ( ) [2 ''( )] 2[2 '( )] 3 '( ) [3 ''( )]' 2[3 '( )]' ' '( ) [ ''( )]'' 2[ '( )]'' y t x t x t y t x t x t y t x t x t       将上面三式相加，得 [ ''( ) 3 '( ) 2 ( )]'' 2[ ''( ) 3 '( ) 2 ( )]' ''( ) 3 '( ) 2 ( ) x t x t x t x t x t x t y t y t y t         考虑到 f (t)  x''(t)  3x'(t)  2x(t),上式右端等于 f ''(t)  2 f '(t) ，故得 y''(t)  3y'(t)  2 y(t0  f ''(t)  2 f '(t) 此即为系统的微分方程。 （2）

解：系统框图中有两个迟延单元，因而该系统为二阶系统。设上方迟延单元的输入为x(), 则各个迟延单元的输出为x9k-1),x(k-2) 左边加法器的输出为 x(k)=f(k)+2x(k-1)-4x(k-2) 即xk)-2x(k-1)+4x(k-2)=fk) 右方加法器的输出为 y(k)=2x(k-1)-x(k-2) 由上式移位可得 -2y(k-1)=2[-2x(k-2)]-【-2x(k-3)] 4y(k-2)=2(4x(k-3]-[4x(k-4)] 将上而三式相加得 y(k)-2y(k-1+4y(k-2) =2[x(k-1)-2x(k-2)+4x(k-3)]-[x(k-20-2x(k-3)+4x(k-4)] 代入()及延时得 y(k)-2y(k-1)+4y(k-2)=2f(k-1)-f(k-2) 此即为系统的差分方程。 125某LT连续系统，其初始状态一定，己知当激励为()时，其全响应 y,(t)=e+cos(),1≥0 若初始状态不变，激励为2f()时，其全响应 y2=2cos(t),t≥0 求初始状态不变，而激励为3()时系统的全响应。 分析首先利用LTⅡ连续系统的特性分别求出系统的零输入响应和零状态响应，再根据系 统的齐次性求出不同的激励的系统的全响应。 解设初始状态下系统的零输入响应为”，()，激励为四时，系统的零状态响应为'0， 则由系统的可分解特性可得 y(t)+yr(t)=e+cos(πt),t≥0 (1) 根据LTΠ系统的齐次性，有 2yr(t)=T[2f()],3yr()=T[3f(t] 则当初始状态不变，激励为2)时，系统的全响应 y.(t)+2yr(t)=2cos(πt),t≥0 (2) 联立(1)(2)两式得

解：系统框图中有两个迟延单元，因而该系统为二阶系统。设上方迟延单元的输入为 x(k) ， 则各个迟延单元的输出为 x9k 1), x(k  2). 左边加法器的输出为 x(k)  f (k)  2x(k 1)  4x(k  2) 即 x(k)  2x(k 1)  4x(k  2)  f (k) 右方加法器的输出为 y(k)  2x(k 1)  x(k  2) 由上式移位可得 4 ( 2) 2(4 ( 3)] [4 ( 4)] 2 ( 1) 2[ 2 ( 2)] [ 2 ( 3)]              y k x k x k y k x k x k 将上而三式相加得 2[ ( 1) 2 ( 2) 4 ( 3)] [ ( 20 2 ( 3) 4 ( 4)] ( ) 2 ( 1 4 ( 2)                 x k x k x k x k x k x k y k y k y k 代入 f (k) 及延时得 y(k)  2 y(k 1)  4 y(k  2)  2 f (k 1)  f (k  2) 此即为系统的差分方程。 1.25 某 LTI 连续系统，其初始状态一定，已知当激励为 f (t) 时，其全响应 ( ) cos( ), 0 1     y t e t t t  若初始状态不变，激励为2 f (t) 时，其全响应 2cos( ), 0 y2  t t  求初始状态不变，而激励为 3 f (t) 时系统的全响应。 分析 首先利用 LTI 连续系统的特性分别求出系统的零输入响应和零状态响应，再根据系 统的齐次性求出不同的激励的系统的全响应。 解 设初始状态下系统的零输入响应为 y (t) x ，激励为 f (t) 时，系统的零状态响应为 y (t) f ， 则由系统的可分解特性可得 ( )  ( )   cos( ),  0  y t y t e t t t x f  （1） 根据 LTI 系统的齐次性，有 2y (t) T[2 f (t)],3y (t) T[3 f (t)] f  f  则当初始状态不变，激励为2 f (t) 时，系统的全响应 y (t)  2 y (t)  2 cos( t),t  0 x f  （2） 联立（1）（2）两式得

y(t)=2e- yr(0=-e'+cos(),1≥0 则初始状态不变，激励为3()时系统的全响应为 y,(t)+3f,(t)=-e-'+3cos(t),120 即y,(0=-e'+3cos(π)，1≥0

t x y t e  ( )  2 ( )    cos( ),  0  y t e t t t f  则初始状态不变，激励为3 f (t) 时系统的全响应为 ( )  3 ( )    3cos( ),  0  y t f t e t t t x f  即 ( ) 3cos( ), 0 3      y t e t t t 

2.2已知描述系统的微分方程和初始状态如下，试求其0，初始值。 y"(t)+4y'()+3y(t)=f"(t)+f().y0.)=2,y(0)=-2,f(t)=8(t) 解：原式=6"()+6) 令y')=a8"(0+b8'(0+c6)+Y 则有y()=a6()+bδ)+y,() y(t)=aδ(t)+y(t) 整理得 aδ"'(t)+[4a+b]6'(t)+[3a+4b+c]δ(t)+[yo(t)+4y(t)+3y,(t)]=8'(t)+δ() a=1 a=-1 4a+b=0→b=-4 3a+4b+c=1c=14 .0)-0.)=8'dt-460dt+0h=-4 y(0.)=-2 y0,)-y0.)=o"0h-46udt+140+r0h=l4 .y(0)=12 2.5已知描述系统的微分方程和初始状态如下，试求其零输入响应、零状态响应和完全响 应。 y"(t)+4y'(t)+4y(t)=f'(t)+3f(t),y(0.)=0,y'(0_)=2,ft)=eε(t) 解：由零输入的性质可知，要求零输入响应即求解微分议程 y"(t)+4y'(t)+4y(t)=0 y(0,)=1y'.(0.)=2 解方程得 y,(0)=C,e2'+C2te2 代入初始值得 y(0)=C1=1 y'.(0,)=-2C1+C2=2 解以上两式得C=1,C2=4,则系统的零输入响应为 y.(t)=e-2+41e-2,t≥0 由零状态响应的性质可知，求零状态响应即求解微分方程 y",(t)+4y',(t)+4y()=δ()+2eε(t) y'r(0_)=y(0.)=0 方程右端含有冲激项，两端对0-到0，积分 [y"y0+4y,0+4y,0=Dδ0)+2e'e)t

2.2 已知描述系统的微分方程和初始状态如下，试求其  0 初始值。 y''(t)  4 y'(t)  3y(t)  f ''(t)  f (t) , y(0 )  2, y'(0 )  2, f (t)   (t)   解：原式  ' '(t)   (t) 令 ' '( ) ' '( ) '( ) ( ) ( ) 0 y t  a t  b t  c t   t 则有 '( ) ( ) ( ) ( ) 1 y t  a t  b t   t ( ) ( ) ( ) 1 y t  a t   t 整理得 ' '( ) [4 ] '( ) [3 4 ] ( ) [ ( ) 4 ( ) 3 ( )] ' '( ) ( ) 2 0 1 a t  a  b  t  a  b  c  t   t   t   t   t   t ∴                       14 4 1 3 4 1 4 0 1 c b a a b c a b a ∴ (0 ) (0 ) '( ) 4 ( ) ( ) 4 0 0 1 0 0 0 0                  y y  t dt  t dt  t dt '(0 ) '(0 ) ''( ) 4 '( ) 14 ( ) ( ) 14 (0 ) 2 0 0 1 0 0 0 0 0 0                        y y t dt t dt t t dt y     ∴ '(0 )  12  y 2.5 已知描述系统的微分方程和初始状态如下，试求其零输入响应、零状态响应和完全响 应。 y''(t)  4 y'(t)  4y(t)  f '(t)  3 f (t), y(0 ) 0, y'(0 ) 2, f (t) e (t) t        解：由零输入的性质可知，要求零输入响应即求解微分议程           (0 ) 1, ' (0 ) 2 ' '( ) 4 '( ) 4 ( ) 0 x x y y y t y t y t 解方程得 t t x y t C e C te 2 2 2 1 ( )     代入初始值得 ' (0 ) 2 2 (0 ) 1 1 2 1         y C C y C x x 解以上两式得 1, 4, C1  C2  则系统的零输入响应为 ( ) 4 , 0 2 2      y t e te t t t x 由零状态响应的性质可知，求零状态响应即求解微分方程              ' (0 ) (0 ) 0 ' ' ( ) 4 ' ( ) 4 ( ) ( ) 2 ( ) f f t f f f y y y t y t y t  t e  t 方程右端含有冲激项，两端对  0 到  0 积分            0 0 0 0 y' ' (t) 4y' (t) 4y (t)dt (t) 2e (t)dt t f f f  