
3.5 Properties of Fourier Transform 根据傅里叶变换的概念,一个非周期信号可以表述为指数 函数的积分,即 f)= F(jw)edω 式中: F(Gw)=f(t)e4dt 时间函数f(t)与频谱函数F(jw)有一一对应的关系,可记为 f(t)←→F(jw) 1
1 根据傅里叶变换的概念,一个非周期信号可以表述为指数 函数的积分, 即 §3.5 Properties of Fourier Transform

3.5傅里叶变换的性质 。线性Linearity 0 奇偶虚实性Conjugation and Conjugate Symmetry 对称性Duality 。尺度变换特性Time Scaling 时移特性和频移特性Time and Frequency Shifting 微分和积分特性Differentiation and Integration 。卷积定理Convolution Property ·Paseval定理Paseval's Relation 2
2 • 线性 Linearity • 奇偶虚实性 Conjugation and Conjugate Symmetry • 对称性 Duality • 尺度变换特性 Time Scaling • 时移特性和频移特性 Time and Frequency Shifting • 微分和积分特性 Differentiation and Integration • 卷积定理 Convolution Property • Paseval定理 Paseval’s Relation 3.5 傅里叶变换的性质

l、线性Linearity 若f(t)→F(j0),f(0)→F(j0), 且设a1,a2为常数,则有 af(t)+a2f(t)>af(j@)+a2(j@) 若则 FT f(t)]=F(@) m三ao立a5o 3
3 1、线性 Linearity 若 则 ( ) () i Fi FT f t n i i i n i FT ai f i t a F 1 1 ( ) () 若 ( ) ( ), ( ) ( ), f 1 t F1 j f 2 t F2 j 且设a1 , a2为常数,则有 ( ) ( ) ( ) ( ) a1 f 1 t a2 f 2 t a1 f 1 j a2 f 2 j
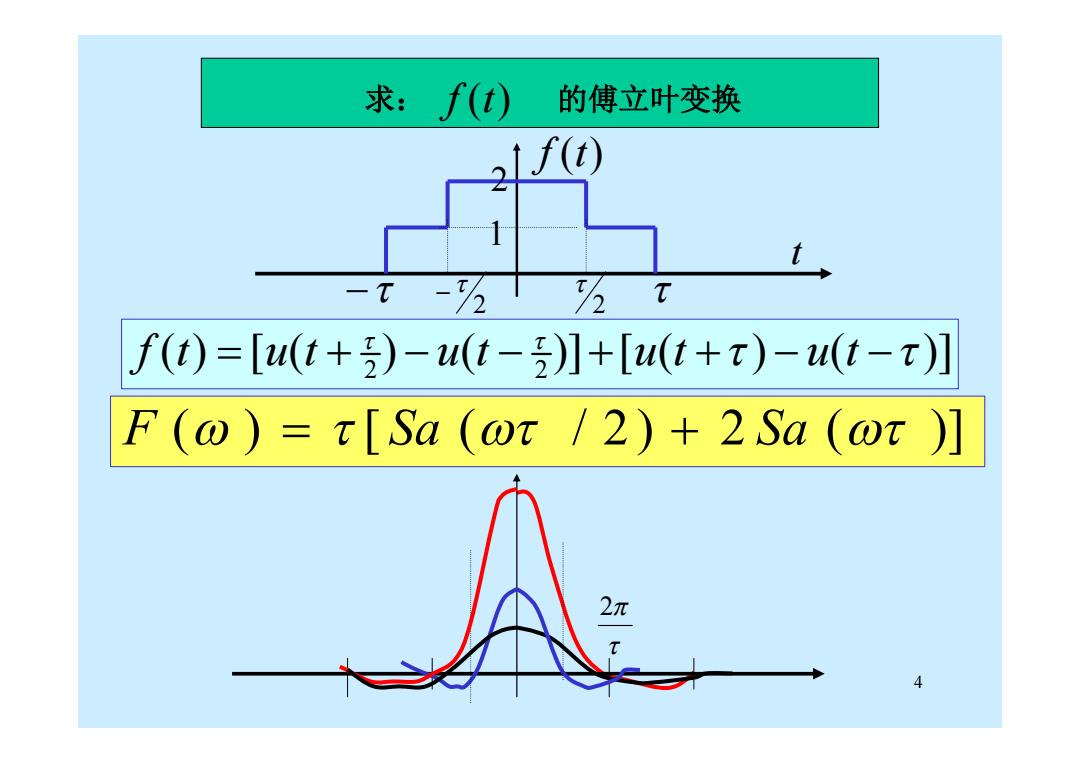
求:f(t) 的傅立叶变换 /(t) -t -92 f(t)=[u(t+)-u(t-)】+[u(t+t)-u(t-T)】 F(@)=t[Sa (ot /2)+2Sa (or ) 4
4 求: f (t) 的傅立叶变换 2 2 f (t) 1 2 t 2 2 f t u t u t u t u t ( ) [ ( ) ( )] [ ( ) ( )] F ( ) [ Sa ( / 2 ) 2 Sa ( )] 2

2、奇偶虚实性 Conjugation and Conjugate Symmetry 无论t)是实函数还是复函数,下面两式均 成立 时域反摺 频域也反摺 FT[f(t)]=F(@) FT[f(-t)]=F(-o) 时域共轭 FT[f(t)]=F(-@) 频域共轭 并且反摺 FTLf(-t)]=F(@) 5
5 2、 奇偶虚实性 Conjugation and Conjugate Symmetry 无论f(t)是实函数还是复函数,下面两式均 成立 [ ( )] ( ) * * FT f t F FT[ f (t)] F() FT[ f (t)] F() [ ( )] ( ) * * FT f t F 时域反摺 频域也反摺 时域共轭 频域共轭 并且反摺