3.做一做:在正方体ABCD-A1B1C1D中,直线BC1与平面A1BD 所成的角的正弦值是 解析:以D为原点,DA,DC,DD的 方向分别为x轴、y轴、轴正方向, A 建立空间直角坐标系,如图,设正方 体的棱长为1,则 D(0,0,0),A1(1,0,1),B(1,1,0),C1(0,1,1)
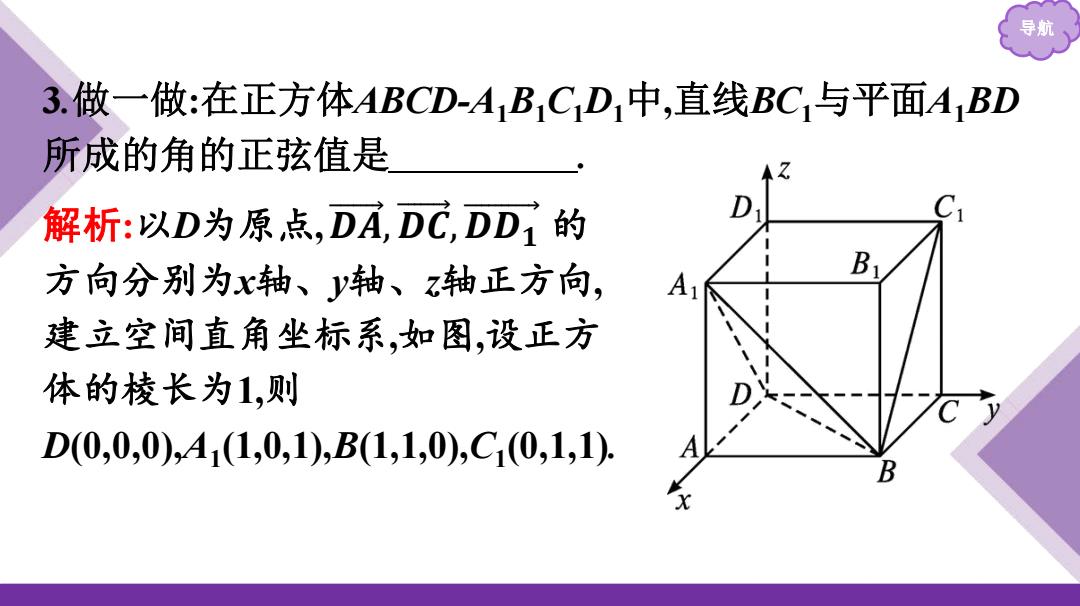
导航 3.做一做:在正方体ABCD-A1B1C1D1中,直线BC1与平面A1BD 所成的角的正弦值是 . 解析:以D为原点, 的 方向分别为x轴、y轴、z轴正方向, 建立空间直角坐标系,如图,设正方 体的棱长为1,则 D(0,0,0),A1 (1,0,1),B(1,1,0),C1 (0,1,1). 𝑫 𝑨 , 𝑫 𝑪 , 𝑫𝑫𝟏

导航 ∴.DA=(1,0,1),DB=(1,1,0),BC1=(-1,0,1), 设n=(化y,z)是平面A1BD的一个法向量, DAin=x+z=0, 则 DBn=x+y=0, 令x=1,得n=(1,-1,1). 设直线BC1与平面A1BD所成的角为O, 则sin64 Hleo<n.ECi斗e== 答案
导航 ∴𝑫𝑨𝟏 =(1,0,1),𝑫 𝑩 =(1,1,0),𝑩𝑪𝟏 =(-1,0,1). 设 n=(x,y,z)是平面 A1BD 的一个法向量, 则 𝑫𝑨𝟏 ·𝒏 = 𝒙 + 𝒛 = 𝟎, 𝑫 𝑩 ·𝒏 = 𝒙 + 𝒚 = 𝟎, ∴x=-y=-z. 令 x=1,得 n=(1,-1,-1). 设直线 BC1与平面 A1BD 所成的角为 θ, 则 sin θ=|cos<n,𝑩𝑪𝟏 >|= 𝒏·𝑩𝑪𝟏 |𝒏||𝑩𝑪𝟏 | = -𝟐 𝟑× 𝟐 = 𝟔 𝟑 . 答案: 𝟔 𝟑

导则 思考辨析】 判断正误(正确的画“√,错误的画“×) (1)直线与平面所成角的取值范围是0°<s90°.( (2)直线与平面所成的角和直线的方向向量与平面的法向量 所成的角相等( (3)斜线与平面的夹角是斜线和这个平面内所有直线所成角 中最小的角.( (4)若直线l与平面a所成角为0,直线的方向向量v与平面a的 法向量n的夹角为<y,n>,则有sin0=cos<v,n>()
导航 【思考辨析】 判断正误.(正确的画“ ”,错误的画“×”) (1)直线与平面所成角θ的取值范围是0°<θ≤90° .( × ) (2)直线与平面所成的角和直线的方向向量与平面的法向量 所成的角相等.( × ) (3)斜线与平面的夹角是斜线和这个平面内所有直线所成角 中最小的角.( ) (4)若直线l与平面α所成角为θ,直线l的方向向量v与平面α的 法向量n的夹角为<v,n>,则有sin θ=|cos<v,n>|.( )

导航 课堂·重难突破 探究一用定义法求线面角 【例1】在正四面体ABCD中,E为棱AD的中点,连接CE,求CE 与平面BCD所成角的正弦值. 分析:只需找到CE在平面BCD内的射影,关键是理清通过,点E 作的垂线,垂足落在何处」
导航 课堂·重难突破 探究一 用定义法求线面角 【例1】在正四面体ABCD中,E为棱AD的中点,连接CE,求CE 与平面BCD所成角的正弦值. 分析:只需找到CE在平面BCD内的射影,关键是理清通过点E 作的垂线,垂足落在何处
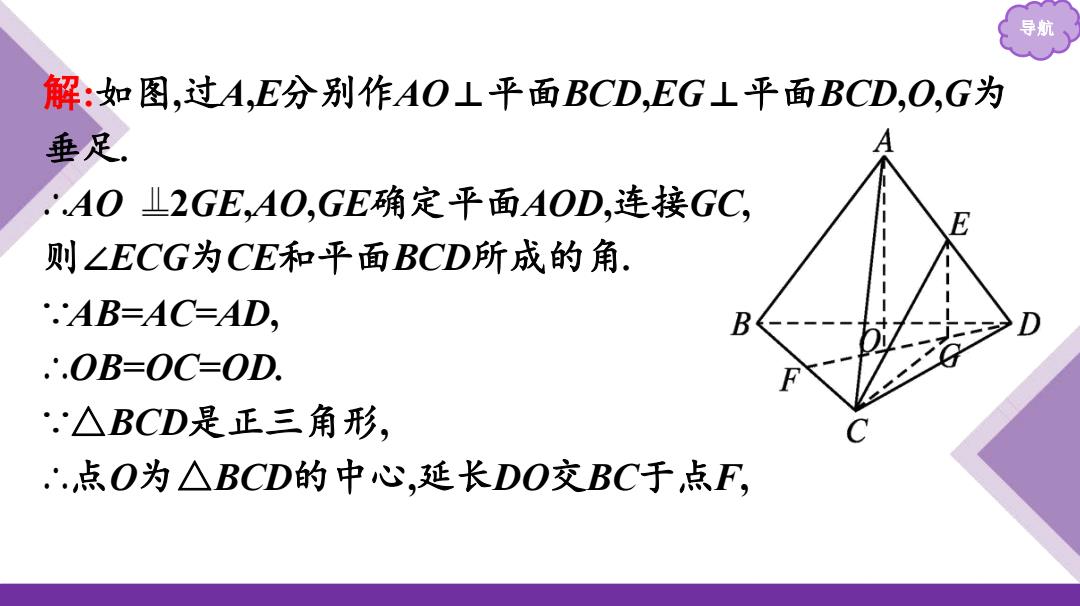
导期 解:如图,过A,E分别作AOL平面BCD,EG⊥平面BCD,O,G为 垂足 'AOL2GE,AO,GE确定平面AOD,连接GC, E 则∠ECG为CE和平面BCD所成的角. .AB=AC=AD, .∴.OB=OC=OD. .△BCD是正三角形, .点O为△BCD的中心,延长DO交BC于点F
导航 解:如图,过A,E分别作AO⊥平面BCD,EG⊥平面BCD,O,G为 垂足. ∴AO 2GE,AO,GE确定平面AOD,连接GC, 则∠ECG为CE和平面BCD所成的角. ∵AB=AC=AD, ∴OB=OC=OD. ∵△BCD是正三角形, ∴点O为△BCD的中心,延长DO交BC于点F