2)斜线与平面所成角的性质 ①如图,OB是OA在平面a内的射影,OMca,0是OA与OM所成 的角,01是OA与OB所成的角,02是OB与OM所成的角,则 cos 0= ②平面的斜线与平面所成的角,是斜线和这个平面内所有直 线所成角中最的角. 3)直线与平面所成的角称为直线和平面的
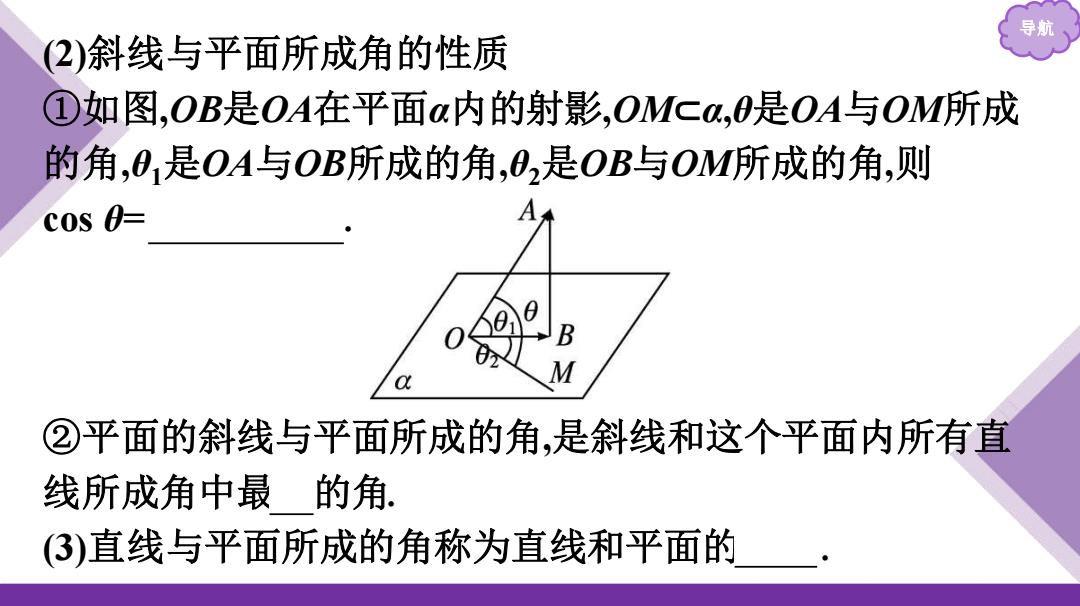
导航 (2)斜线与平面所成角的性质 ①如图,OB是OA在平面α内的射影,OM⊂α,θ是OA与OM所成 的角,θ1是OA与OB所成的角,θ2是OB与OM所成的角,则 cos θ= cos θ1 cos θ2 . ②平面的斜线与平面所成的角,是斜线和这个平面内所有直 线所成角中最小的角. (3)直线与平面所成的角称为直线和平面的夹角

导航 3.做一做:在正方体ABCD-A1BC1D1中,O为侧面BCC1B1的中 心,则AO与平面ABCD所成角的正弦值为( 3 A. B D
导航 3.做一做:在正方体ABCD-A1B1C1D1中,O为侧面BCC1B1的中 心,则AO与平面ABCD所成角的正弦值为( ) A. 𝟑 𝟑 B.𝟏 𝟐 C. 𝟔 𝟔 D. 𝟑 𝟐

导航 解析:如图,设BC的中点为E,连接AE,OE,易知AE⊥OE,则 ∠OAE就是AO与平面ABCD所成角. D 设正方体的棱长为 在Rt△0AE中,AE=a2+()》 2 a 5 2 40=2+(臣a) 6 D = 2 .0Eza…sin∠0AE- OE = V6 6 答案:C
导航 解析:如图,设BC的中点为E,连接AE,OE,易知AE⊥OE,则 ∠OAE就是AO与平面ABCD所成角. 设正方体的棱长为a. 在 Rt△OAE 中,∵AE= 𝒂𝟐 + 𝒂 𝟐 𝟐 = 𝟓 𝟐 a, AO= 𝒂 𝟐 𝟐 + 𝟓 𝟐 𝒂 𝟐 = 𝟔 𝟐 a, ∴OE=𝟏 𝟐 a.∴sin∠OAE=𝑶𝑬 𝑨𝑶 = 𝟔 𝟔 . 答案:C

导 二、借助直线的方向向量、平面的法向量研究直线与平面所 成角的关系 【问题思考】 1.直线l是平面a的一条斜线,v是的一个方向向量,u是平面a的 一个法向量,<y,>和1与a所成的角0有什么关系? 提示:07<y,心或0=<y,>7
导航 二、借助直线的方向向量、平面的法向量研究直线与平面所 成角的关系 【问题思考】 1.直线l是平面α的一条斜线,v是l的一个方向向量,u是平面α的 一个法向量,<v,u>和l与α所成的角θ有什么关系? 提示:θ= 𝛑 𝟐 -<v,u>或 θ=<v,u>- 𝛑 𝟐

导航 2.填空:若v是直线1的一个方向向量,n是平面a的一个法向 量,设直线1与平面a所成角大小为0,则0= .特别地,cos0= ,sin 0=
导航 2.填空:若 v 是直线 l 的一个方向向量,n 是平面 α 的一个法向 量,设直线 l 与平面 α 所成角大小为 θ,则 θ= 𝛑 𝟐 -<v,n>或 θ=<v,n>- 𝛑 𝟐 .特别地,cos θ= sin<v,n> ,sin θ= |cos<v,n>|