《线性代数》课程教学课件（PPT讲稿）第一章 行列式 1.1 行列式的定义

411七1+412X2= 21X1+a22X2 =b2 b D:=b2 12 图 D2= 411 b

       . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b , 2 22 1 12 1 b a b a D         . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b . 21 2 11 1 2 a b a b D 

则二元线性方程组的解为 bi 12 D b2 422 X1= D2 421 D 01 12 X2= D 411 12 L21 L22 L21 L22 注意 分母都为原方程组的系数行列式

则二元线性方程组的解为 , 21 22 11 12 2 22 1 12 1 1 a a a a b a b a D D x   注意 分母都为原方程组的系数行列式. . 21 22 11 12 21 2 11 1 2 2 a a a a a b a b D D x  

例1求解二元线性方程组 3x1-2x2=12, 2x1+x2=1. 解 =3-（-4)=7≠0， D1\ X1= D-14 =D=-21= D 7 4=2,X2=D =-3. 7

       2 1. 3 2 12, 1 2 1 2 x x x x 求解二元线性方程组 解 2 1 3  2 D   3  (4)  7  0, 1 1 12 2 1  D   14, 2 1 3 12 D2   21, D D x 1  1  2, 7 14   D D x 2 2  3. 7 21    

类似地，由三元线性方程组 111+412X2+013X3=b1, 21七1+02七2+4233=b2, (1-2) 031K1+432x2+033七3=b3; (1)引入记号 w 2 3 021 a22 023 31 L32 33 称之为三阶行列式

称之为 . 由三元线性方程组 11 1 12 2 13 3 1 21 1 22 2 23 3 2 31 1 32 2 33 3 3 , , 1 2 ; a x a x a x b a x a x a x b a x a x a x b                （ ） 11 12 13 21 22 23 31 32 33 a a a a a a a a a 类似地

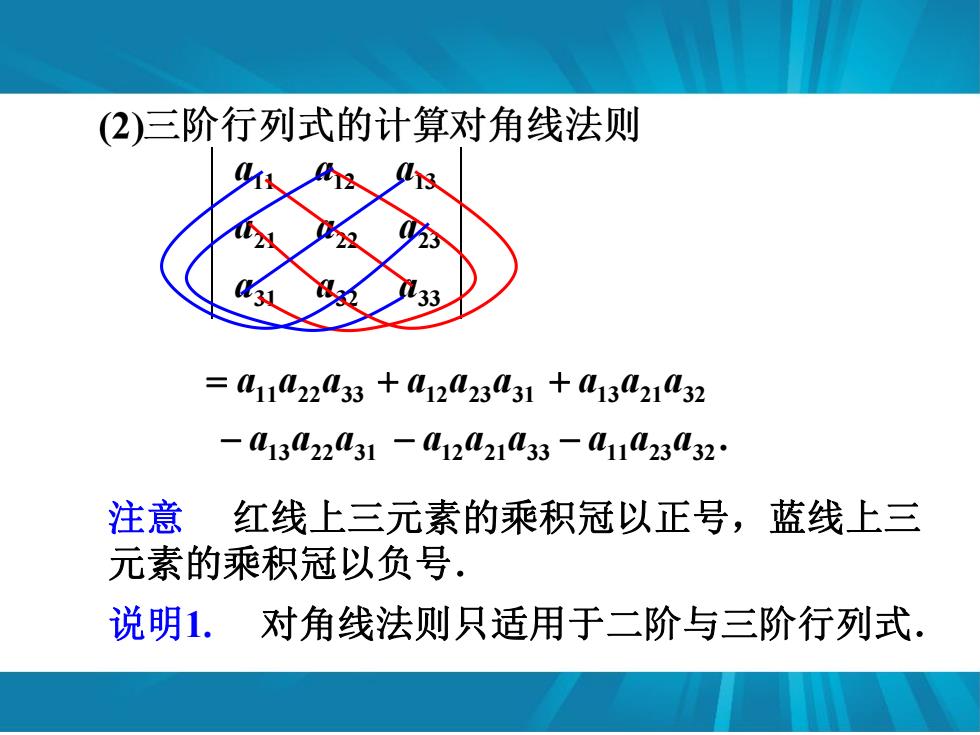
(2)三阶行列式的计算对角线法则 33 =41102233+41223431+013L21032 -L13L22L31-012L21L33-L11L23L32 注意红线上三元素的乘积冠以正号，蓝线上三 元素的乘积冠以负号. 说明1.对角线法则只适用于二阶与三阶行列式

31 32 33 21 22 23 11 12 13 a a a a a a a a a 11 22 33  a a a . 11 23 32  a a a 注意 红线上三元素的乘积冠以正号，蓝线上三 元素的乘积冠以负号． 说明1. 对角线法则只适用于二阶与三阶行列式． 13 21 32  a a a 12 23 31  a a a 13 22 31  a a a 12 21 33  a a a