《线性代数》课程教学课件（PPT讲稿）第三章 矩阵的运算 3-2 逆矩阵

§3.2逆矩阵 一、逆矩阵的定义 二、矩阵可逆的充要条件 三、可逆矩阵的性质 四、典型例题

§3.2 逆矩阵 一、逆矩阵的定义 二、矩阵可逆的充要条件 四、典型例题 三、可逆矩阵的性质

一、逆矩阵的定义 定义3.2.1设A是一个n阶方阵，若存在n阶方阵B,使得 AB=BA=E 则称A可逆的，并称B为A的逆矩阵 例如 4e=[A月 有AB=BA=E,所以A与B互为逆阵. 说明：(1)若A是可逆矩阵，则A的逆矩阵是唯一的

定义3.2.1 设A是一个n阶方阵,若存在n阶方阵B,使得 AB = BA = E 则称 A 可逆的，并称B 为 A 的逆矩阵. 一、逆矩阵的定义 1 2 5 2 , 2 5 2 1 A B     − = =         − 有AB = BA = E ，所以A 与 B 互为逆阵. 例如 说明: (1)若A是可逆矩阵，则A的逆矩阵是唯一的

若设B和C是A的可逆矩阵，则有 AB=BA=E,AC=CA=E, 可得B=EB=(CA)B=C(AB)=CE=C, 所以A的逆矩阵是唯一的，记作A1B=C=A (2)上述等式中A和B的地位是对称的. 3)并不是任意一个矩阵都是可逆矩阵. 下面我们讨论矩阵可逆的条件

若设B和C是A的可逆矩阵，则有 AB = BA = E, AC = CA = E, 可得 B = EB = (CA)B = C(AB) = CE = C. 所以A的逆矩阵是唯一的,记作A -1 1 B C A . − = = (3)并不是任意一个矩阵都是可逆矩阵. 下面我们讨论矩阵可逆的条件。 (2)上述等式中A和B的地位是对称的

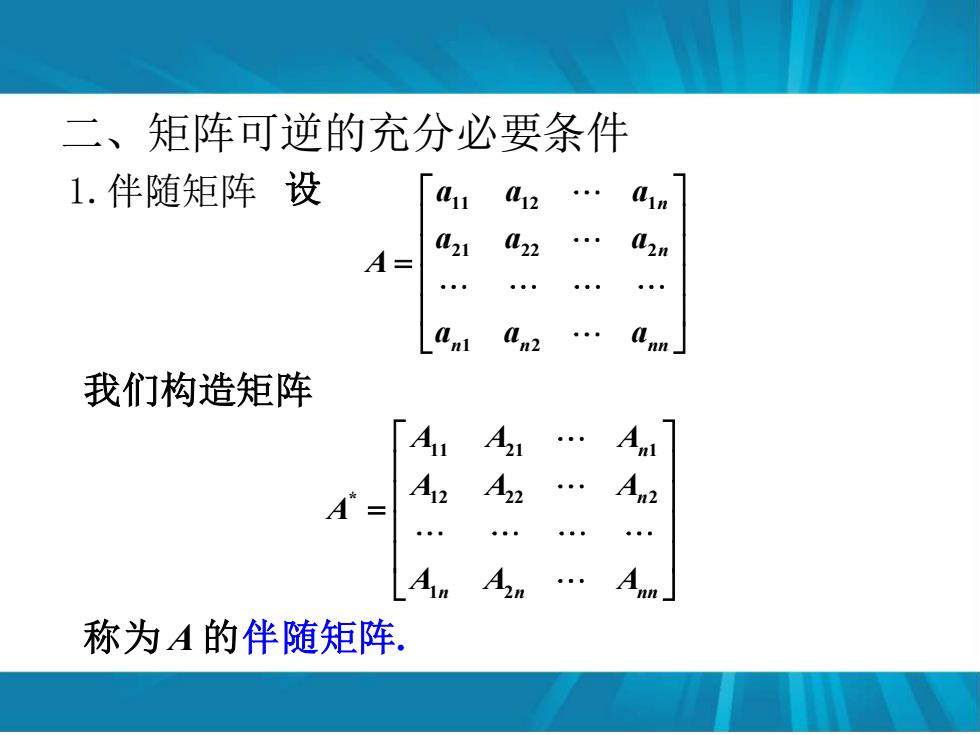
二、矩阵可逆的充分必要条件 1.伴随矩阵设 41 12 A= 21 422 nn- 我们构造矩阵 A A . An A三 An 称为A的伴随矩阵

我们构造矩阵 称为 A 的伴随矩阵. 设 11 12 1 21 22 2 1 2 n n n n nn a a a a a a A a a a       =       二、矩阵可逆的充分必要条件 1.伴随矩阵 11 21 1 * 12 22 2 1 2 n n n n nn A A A A A A A A A A       =      

1.说明：（①）A中元素是A中各元素的代数余子式。 (2)A中各元素的代数余子式的排列顺序问题， 行的余子式按列排或列的余子式按行排 12-1 例题1、求矩阵=310 的伴随矩阵 -10-2 A1=-2,A21=4,A1=1 [-2 41 42=6A2=-3,42=-3A= 6 -3 -3 A13=1,A3=-2,A3=-5 1 -2 -5

例题1、求矩阵 的伴随矩阵.           − − − = 1 0 2 3 1 0 1 2 1 A * 2 4 1 6 3 3 1 2 5 A   −   = − −       − − 1.说明：(1)A * 中元素是A中各元素的代数余子式。 . (2) 行的余子式按列排或列的余子式按行排 A中各元素的代数余子式的排列顺序问题， 2, A11 = − 4, A21 = A31 =1 1, A13 = 2, A23 = − 5 A33 = − 3, A12 = 6, A22 = − A32 = −3