
20 引入乘子函数2,(x)构造新泛函 *=(5+2p,)d=F*a (7) 这样就把条件极值的变分问题化成了无条件极值的变分 问题。对于泛函ⅴ*来说,其欧拉方程组为 F-F,=0 (j=1,2,…,n) (8) 0,=0 (i=1,2,…,m) 数学建模·
引入乘子函数 (x) i 构造新泛函 = + = = 1 0 1 0 * ( ) * 1 x x x x m i i i v F dx F dx (7) 这样就把条件极值的变分问题化成了无条件极值的变分 问题。对于泛函v *来说,其欧拉方程组为 = = − = = 0 ( 1,2, , ) 0 ( 1,2, , ) * ' * i m F F j n i dx y d yi j (8)
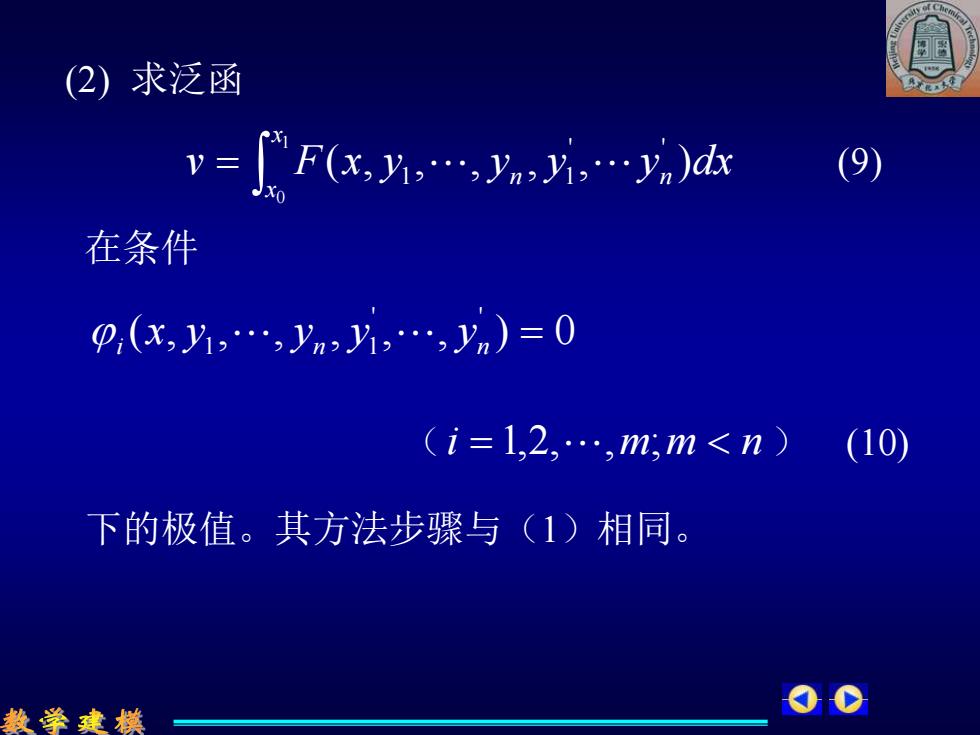
(2)求泛函 v=Fx,达 在条件 0,(x,y,…,yn,,,yn)=0 (i=1,2,…,m,m<n) (10) 下的极值。其方法步骤与(1)相同。 数学建模
(2) 求泛函 v F x y y y y dx n x x n ( , , , , , ) ' ' 1 1 1 0 = (9) 在条件 ( , , , , , , ) 0 ' ' i x y1 yn y1 yn = (i = 1,2,,m;m n ) (10) 下的极值。其方法步骤与(1)相同

(3)求泛函 v=广F(x,n,…y)d (11) 在所谓等周条件 =(d =1 (12) (i=1,2,,m) 下的极值问题。其中Z,为常数,m可以大于、小于 或等于n。 数学建棋
(3) 求泛函 v F x y y y y dx n x x n ( , , , , , ) ' ' 1 1 1 0 = (11) 在所谓等周条件 n i x x i n v = F x y y y y dx = l ( , , , , , ) ' ' 1 1 1 0 (12) (i = 1,2,,m ) 下的极值问题。其中 i l 为常数, m 可以大于、小于 或等于n