
2.最简泛函的变分 设y(x)、Y(x)∈D,则称δy=Y(x)-y(x)为函数 y(x)的变分。即函数的变分δy反映的是整个函数的改变。 函数的变分δy有如下重要性质: 如果y(x)和Y都可导,则 ()'=[Y(x)-y(x)]'=Y'(x)-y'(x)=y 即函数变分的导数等于函数导数的变分。 00 数学建棋
2. 最简泛函的变分 设 y(x) 、 Y (x) D ,则称 y = Y (x) − y(x) 为函数 y(x) 的变分。即函数的变分 y 反映的是整个函数的改变。 函数的变分 y 有如下重要性质: 如果 y(x) 和Y 都可导,则 (y)'= [Y (x) − y(x)]'= Y '(x) − y'(x) = y' 即函数变分的导数等于函数导数的变分
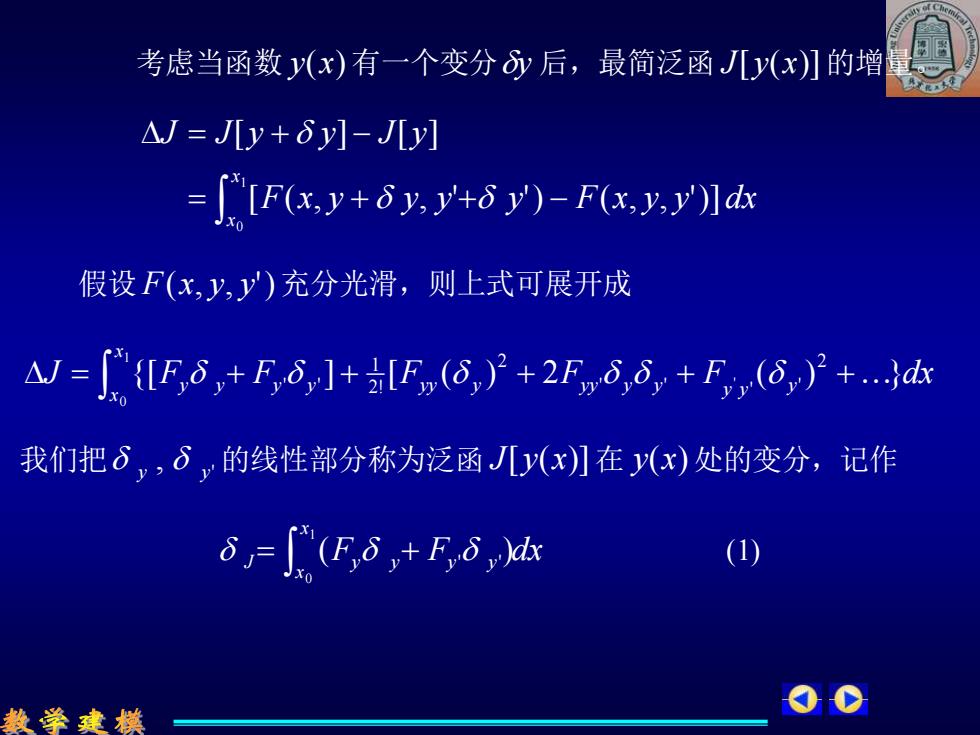
考虑当函数y(x)有一个变分后,最简泛函JLy(x)]的增 △J=JLy+δy]-JLy] =["[F(x,y+8y.y+6)-F(x.y.y)ds 假设F(x,y,y)充分光滑,则上式可展开成 △=∫{F,δ+F5]+[F,(⑥,}+2F,5,6+F,(⊙,》+ 我们把8,δ,的线性部分称为泛函JLy(x)]在(x)处的变分,记作 δ=∫(F3+F6k 数学建模
考虑当函数 y(x) 有一个变分y 后,最简泛函 J[ y(x)] 的增量。 F x y y y y F x y y dx J J y y J y x x = + + − = + − 1 0 [ ( , , ' ') ( , , ')] [ ] [ ] 假设 F(x, y, y') 充分光滑,则上式可展开成 = + + + + + 1 0 {[ ] [ ( ) 2 ' ( ) } 2 ' ' ' ' 2 2! 1 ' ' x x y y y y y y y yy y yy y y J F F F F F dx 我们把 ' , y y 的线性部分称为泛函 J[ y(x)] 在 y(x) 处的变分,记作 F F dx x x J = y y + y y 1 0 ( ) ' ' (1)
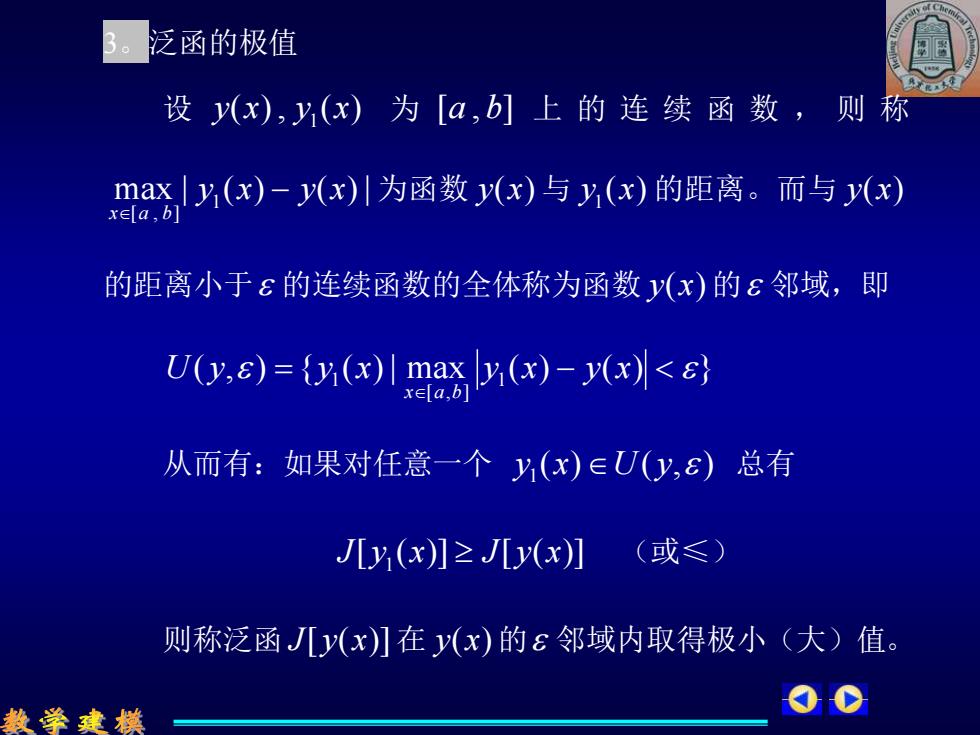
3。泛函的极值 设y(x),y,(x)为[a,b]上的连续函数,则称 max|,(x)-y(x)川为函数(x)与y,(x)的距离。而与y(x) x∈[a,b] 的距离小于ε的连续函数的全体称为函数y(x)的8邻域,即 U0g,8)={(m()-x<} 从而有:如果对任意一个y(x)∈U(y,)总有 J[y(x)]≥JLy(x)] (或≤) 则称泛函J兀y(x)]在y(x)的ε邻域内取得极小(大)值。 数学建模
3。泛函的极值 设 ( ) , ( ) 1 y x y x 为 [a , b] 上 的 连 续 函 数 , 则 称 max | ( ) ( ) | 1 [ , ] y x y x x a b − 为函数 y(x) 与 ( ) 1 y x 的距离。而与 y(x) 的距离小于 的连续函数的全体称为函数 y(x) 的 邻域,即 ( , ) { ( ) | max ( ) ( ) } 1 [ , ] 1 = − U y y x y x y x x a b 从而有:如果对任意一个 ( ) ( , ) 1 y x U y 总有 [ ( )] [ ( )] 1 J y x J y x (或≤) 则称泛函 J[ y(x)] 在 y(x) 的 邻域内取得极小(大)值

泛函极值的必要条件—欧拉方程 对于泛函J(x=广F(x,y,y)d(x)∈D) 关于泛函极值的必要条件有如下结论: 定理1 若泛函Jy(x)]在y(x)的ε邻域内取得 极值,则泛函在y(x)处的变分δ,=0。 定理2泛函极值的必要条件为 F,-岳F=0 (2〉 此方程就是欧拉方程。 教学建模
泛函极值的必要条件—欧拉方程 对于泛函 = 1 0 [ ( )] ( , , ') x x J y x F x y y dx( y(x) D ), 关于泛函极值的必要条件有如下结论: 定理 1 若泛函 J[ y(x)] 在 y(x) 的 邻域内取得 极值,则泛函在 y(x) 处的变分 J = 0 。 定理 2 泛函极值的必要条件为 − y' = 0 dx d Fy F (2) 此方程就是欧拉方程

欧拉方程的另一种形式为 E-Fx-yFyy-y"Ey=0 当F,y≠0时,欧拉方程为一个二阶微分方程,积 分后有两个任意常数,可由两个边界条件来确定。 数学建棋
欧拉方程的另一种形式为 Fy − Fy'x − y'Fy' y − y''Fy' y' = 0 当 Fy' y' 0 时,欧拉方程为一个二阶微分方程,积 分后有两个任意常数,可由两个边界条件来确定