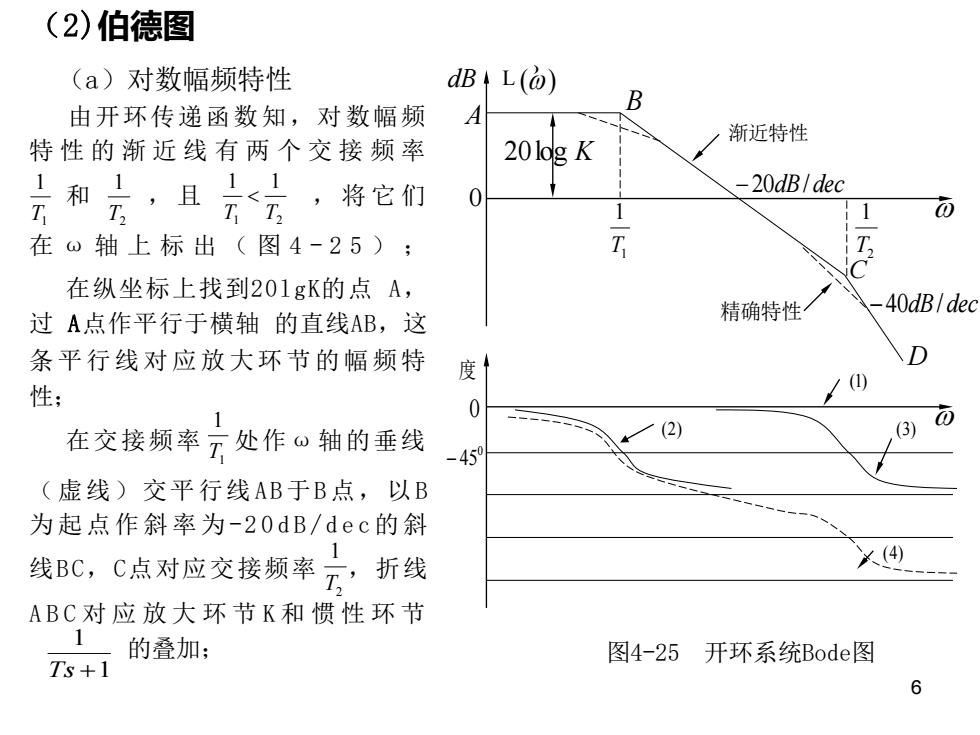
(2)伯德图 (a)对数幅频特性 dB L() 由开环传递函数知,对数幅频 A B 20l0g K 渐近特性 特性的渐近线有两个交接频率 无和名,且行,将它们 0 -20dB/dec 1 ō 在o轴上标出(图4-25); T 在纵坐标上找到201gK的点A, 精确特性 40dB/dec 过A点作平行于横轴的直线AB,这 条平行线对应放大环节的幅频特 D 度1 () 性; 0 在交接频率方处作0轴的垂线 (2) (3 -459 (虚线)交平行线AB于B点,以B 为起点作斜率为-20dB/dec的斜 线BC,C点对应交接频率元,折线 ×(4) ABC对应放大环节K和惯性环节 1 的叠加; 图4-25开环系统Bode图 Ts+1 6
6 (2)伯德图 (a)对数幅频特性 由开环传递函数知,对数幅频 特 性 的 渐 近 线 有 两 个 交 接 频 率 和 , 且 , 将它们 在 ω 轴上标出 ( 图 4 - 2 5 ) ; 在纵坐标上找到20lgK的点 A, 过 A点作平行于横轴 的直线AB,这 条平行线对应放大环节的幅频特 性; 在交接频率 处作ω 轴的垂线 (虚线)交平行线 A B 于B 点, 以B 为起点作斜率为-2 0 d B / d e c 的斜 线B C,C点对应交接频率 ,折线 ABC 对 应 放 大 环 节 K 和 惯 性 环 节 的叠加; 1 2 1 1 T T 1 1 T 2 1 T 1 1 Ts + 1 1 T 2 1 T 图4-25 开环系统Bode图 dBA 0 20log K B −20dB/ dec C 渐近特性 D L() 1 1 T 精确特性 2 1 T −40dB/ dec 度 0 − 450 L () (4) (2) (1) (3)

以C为起点,作斜率为-40dB/dec的斜线CD,折线ABCD即为系统开环对 数幅频特性的渐近线。 (b)对数相频特性 在图4-25上分别画出三个环节的相频特性曲(图中(1)-放大环节, (2)-惯性环节1和(3)-惯性环节2),然后将它们在纵轴方向上相加 得到系统开环相频特性曲线(4)。 例4-2试绘制传递函数为 G(s)= Kv (4-93) S G2(s)= 2 (4-94) 的对数幅频特性
7 以C为起点,作斜率为-40dB/dec的斜线CD,折线ABCD即为系统开环对 数幅频特性的渐近线。 (b)对数相频特性 在图4-25上分别画出三个环节的相频特性曲(图中(1)-放大环节, (2)-惯性环节1和(3)-惯性环节2) ,然后将它们在纵轴方向上相加 得到系统开环相频特性曲线(4)。 例4-2 试绘制传递函数为 (4-93) (4-94) 的对数幅频特性。 s K G s V 1 ( ) = 2 2 ( ) s K G s a =

解:由前面介绍的积分环节的对数幅频特性知,当有个积分环节串联时, 对数幅频特性应是一条过横轴上o=1且斜率为-n×20dB/dec的直线。 式4-93)和(4-94)中分别含有一个和两个积分环节(串联),当 不考虑K和K的影响时,它们的对数幅频特性应是过o=1且斜率分别 为-0dB/dec和-40dB/dec的直线,如图4-26和图4-27中虚线所示。考虑 到K和K的作,上述两条直线应分别在纵轴方向上平移201gK和201gK。 分贝(如图中实线所示),即o=1所对应的坐标值应分别为201gK和 201gK分贝。设对数幅频特性与零分贝线(横轴)的交点频率值分别 为o和⊙a,则有 201gG,0)-a,=201g =20lgK,-20g0,=0(4-95) 20e.Ua)=20e =20gK。-20go2=0(4-96) 8
8 解: 由前面介绍的积分环节的对数幅频特性知,当有n个积分环节串联时, 对数幅频特性应是一条过横轴上ω=1且斜率为 -n×20dB/dec的直线。 式4-93)和( 4-94 )中分别含有一个和两个积分环节(串联),当 不考虑KV和Ka的影响时,它们的对数幅频特性应是过ω=1 且斜率分别 为-0dB/dec和-40dB/dec的直线,如图4-26和图4-27中虚线所示。考虑 到KV和Ka的作,上述两条直线应分别在纵轴方向上平移20lgKv和20lgKa 分贝(如图中实线所示 ),即ω=1所对应的坐标值应分别为20lgKv和 20lgKa分贝。设对数幅频特性与零分贝线(横轴)的交点频率值分别 为ω v和ω a,则有 (4-95) 和 (4-96) 20lg ( ) 20lg 20lg 20lg 0 1 = = − = = = v v v K j K G j v v 20lg ( ) 20lg 20lg 20lg 0 2 2 2 = = − = = = a a a K K G j a a