
二、行列式按行(列)展开法则1. 引理若n级行列式D= det(a)的中第i 行所有元素除a外都为0,则D=a,AjF82.6行列式按一行(列)展开
§2.6 行列式按一行(列)展开 元素除 aij 外都为 0,则 . D a A = ij ij 1.引理 二 、行列式按行(列)展开法则 若n 级行列式 D = det( ) aij 的 中第 i 行所有

证:先证a=an的情形,即aniaina1,n-1..D=an-1,nan-1,n-1n-1,100ann由行列式的定义,有E (-)ai-m.D=+ji.jnE (-1) -" u2.-1/.-.mji.jn--nZ (-- -..=annj..jn-1Rs2.6行列式按一行(列)展开
§2.6 行列式按一行(列)展开 证:先证 a a ij nn = 的情形,即 11 1, 1 1 1,1 1, 1 1, 0 0 n n n n n n n nn a a a D a a a a − − − − − = 由行列式的定义,有 1 1 2 1 1 2 ( ) 1 2 1, ( 1) n n n n j j j j n j nj j j j D a a a a − − = − 1 1 1 2 1 1 1 ( ) 1 2 1, ( 1) n n n j j n j j n j nn j j n a a a a − − − = − − 1 1 1 1 1 1 ( ) 1 1, ( 1) n n n j j nn j n j j j a a a − − − = − −
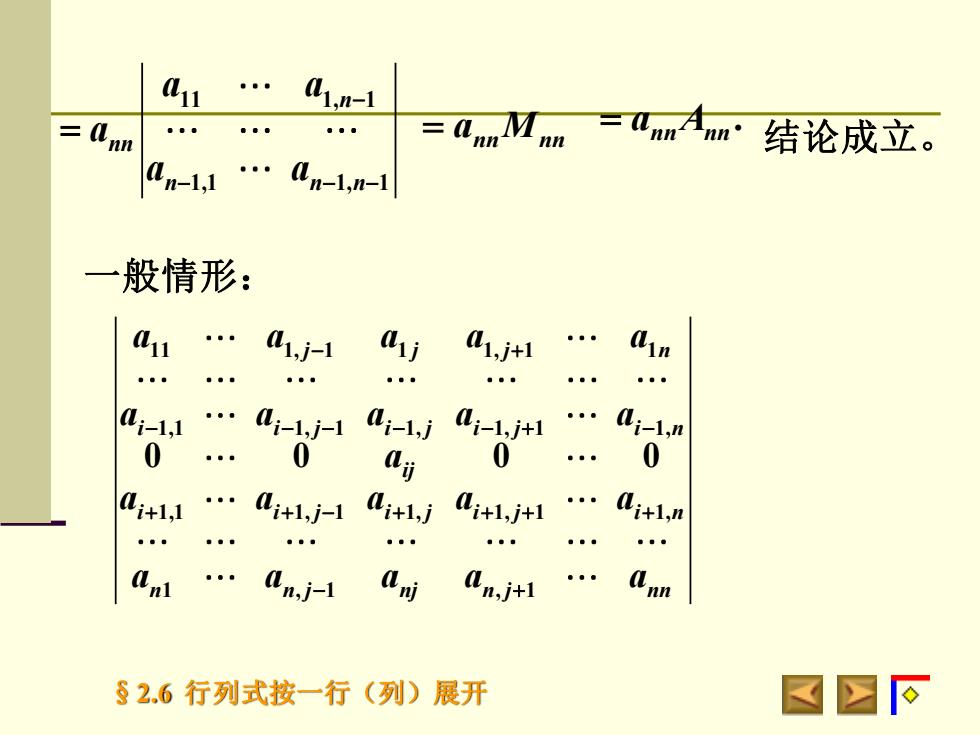
auan-1M=a=ann结论成立。nnnnnnan-1,1an-1,n-1-般情形:anavjaina1,j-1al,j+1..a,-1,1 . a-1,j-1a;-1,ja;-1,j+1a;-1,n0000aiai+1,1... ai+1,j-1ai+1,nai+1,ja;+1,j+1anian,j+1annan,j-1.R$2.6行列式按一行(列)展开
§2.6 行列式按一行(列)展开 11 1, 1 1,1 1, 1 n nn n n n a a a a a − − − − = . nn nn = a A nn nn = a M 结论成立。 一般情形: 11 1, 1 1 1, 1 1 1,1 1, 1 1, 1, 1 1, 1,1 1, 1 1, 1, 1 1, 1 , 1 , 1 0 0 0 0 j j j n i i j i j i j i n ij i i j i j i j i n n n j nj n j nn a a a a a a a a a a a a a a a a a a a a a − + − − − − − + − + + − + + + + − +

aiianja1,j+1ainai,j-1·+*-+ati-1,j-1at;-1,na;-1,1ai-1,j(t;-1,j+1=(-1)"-a;+1,1.. ai+1,j-1a;+1,nai+1,jai+1,j+1anannanjan,j-1an,j+10000..aijanavja1,j-1a,j+1ain....·.ai-1, .. ai-1,j-1 ai-1,j+1.. ai-l,na;-1,j=(-1)n-i(-1)"-jai+1,1.. ai+1,j-1ai+1,j+1... ai+1,nai+1,j....anannan,j+1anj...an,j-1·0000aj.=(-1)2n-(i+i)a,M, =(-1)i+i a,Mj= a,(-1)i+i M, = ajAj.结论成立。Fs2.6行列式按一行(列)展开
§2.6 行列式按一行(列)展开 11 1, 1 1, 1 1 1 1,1 1, 1 1, 1 1, 1, 1,1 1, 1 1, 1 1, 1, 1 , 1 , 1 ( 1) ( 1) 0 0 0 0 j j n j i i j i j i n i j n i n j i i j i j i n i j n n j n j nn nj ij a a a a a a a a a a a a a a a a a a a a a − + − − − − + − − − − + + − + + + + − + = − − ( 1)i j ij ij a M + = − 2 ( ) ( 1) n i j ij ij a M − + = −( 1) . i j ij ij ij ij a M a A + = − = 结论成立。 11 1, 1 1 1, 1 1 1,1 1, 1 1, 1, 1 1, 1,1 1, 1 1, 1, 1 1, 1 , 1 , 1 ( 1) 0 0 0 0 j j j n i i j i j i j i n n i i i j i j i j i n n n j nj n j nn ij a a a a a a a a a a a a a a a a a a a a a − + − − − − − + − − + + − + + + + − + = −