一、 罗尔定理 注记1:若罗尔定理的三个条件有一个不成立,则定理的结论可能不成立 f(x)=x0<x<1)满足(1)和(2),但不满足(3)结论不成立 fx)=x,x∈[-1,]满足(1)和(3),但不满足(2)结论不成立 f(x)=x,x∈[-1,]满足(1)和(2),不满足(3),但结论成立
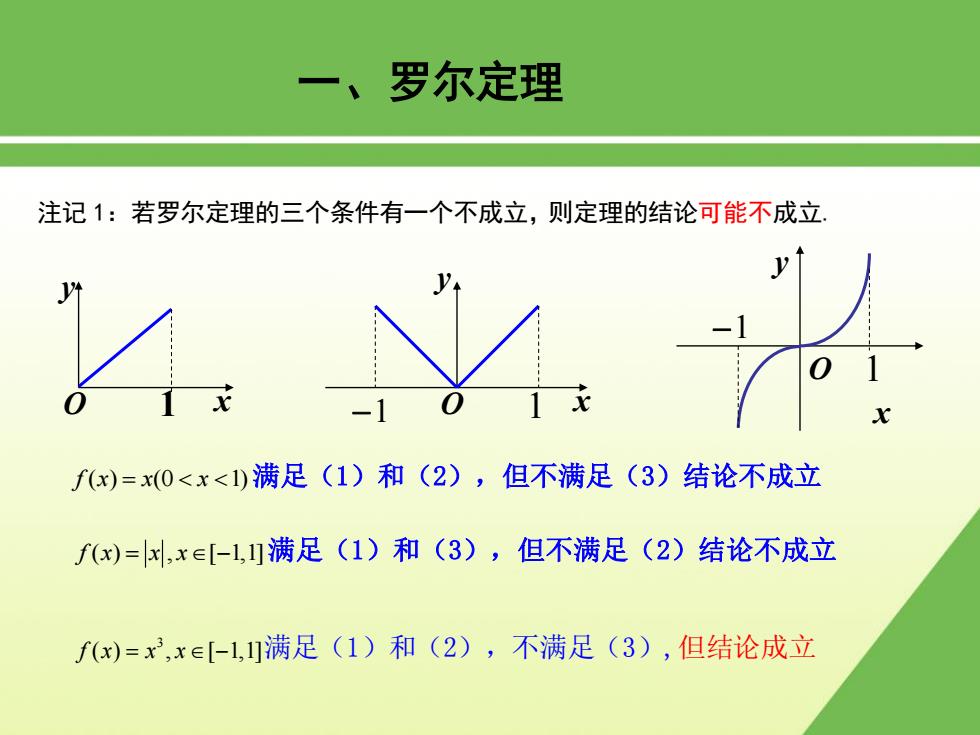
注记 1:若罗尔定理的三个条件有一个不成立, 一、罗尔定理 则定理的结论可能不成立. f x x x ( ) (0 1) 满足(1)和(2),但不满足(3)结论不成立 1 x y O 1 y O 1 x y x O 1 1 f x x x ( ) , [ 1,1] 满足(1)和(3),但不满足(2)结论不成立 3 f x x x ( ) , [ 1,1] 满足(1)和(2),不满足(3),但结论成立

一、罗尔定理 注记2:若函数fx)在[a,b]上连续,在(a,b)内可导且fa=fb).则 方程f'(x)=0在(a,b至少有一个实根 罗尔定理的应用 1.判断一个方程fx)=0在某开区间内至多有几个根. 2.已知函数fw),判断方程f(x)=0根的个数
罗尔定理的应用 1. 判断一个方程 f x( ) 0 在某开区间内至多有几个根. 一、罗尔定理 2. 已知函数 f x( ),判断方程 f x ( ) 0 根的个数. 注记 2:若函数 f x( )在[ , ] a b 上连续,在( , ) a b 内可导且 f a f b ( ) ( ) .则 方程 f x ( ) 0 在( , ) a b 至少有一个实根