
8定理1.(Abel定理)若幂级数Zann=0在x=xo点收敛,则对满足不等式|xxo的一切x幂级数都绝对收敛反之,若当x=xo时该幂级数发散,则对满足不等式[x|>|xo「的一切x,该幂级数也发散证:设anx 收敛,则必有lim anx=0,于是存在n-00n=0常数 M>0,使anx≤M (n=1,2,..)
o x 定理 1. ( Abel定理 ) 若幂级数 n=0 n n a x 则对满足不等式 的一切 x 幂级数都绝对收敛. 反之, 若当 的一切 x , 该幂级数也发散 . 时该幂级数发散 , 则对满足不等式 证: 设 收敛, 则必有 于是存在 常数 M > 0, 使 阿贝尔 目录 上页 下页 返回 结束

nnrxx≤M?xoXoxo80当|x|<x0时,ZM|"收敛,·anxn也收敛,xon=0n=0故原幂级数绝对收敛。反之,若当x=xo时该幂级数发散,下面用反证法证之假设有一点x,满足x>xo「且使级数收敛,则由前面的证明可知,级数在点x。也应收敛,与所设矛盾,故假设不真.所以若当x=xo时幂级数发散,则对一切满足不等式x>xo|的x,原幂级数也发散.证毕olelolol
当 时, 0 x x 收敛, 故原幂级数绝对收敛 . 也收敛, 反之, 若当 0 x = x 时该幂级数发散 ,下面用反证法证之. 假设有一点 1 x 1 0 x x 0 x 满足不等式 0 x x 所以若当 0 x = x 满足 且使级数收敛 , 面的证明可知, 级数在点 故假设不真. 的 x , 原幂级数也发散 . 时幂级数发散 , 则对一切 则由前 也应收敛, 与所设矛盾, n n n n n n x x a x a x 0 = 0 n n n x x a x 0 0 = 证毕 机动 目录 上页 下页 返回 结束
一几何说明幂级数收敛的特性收敛区域发散区域发散区域+x0-RR发悠敛点黛8推论如果幂级数a,x"不是仅在x=0一点收敛,n=0也不是在整个数轴上都收敛.则必有一个完全确定的正数R存在,它具有下列性质:当[x<R时,幂级数绝对收敛;当[x>R时,幂级数发散;当|x=R时,幂级数可能收敛也可能发散
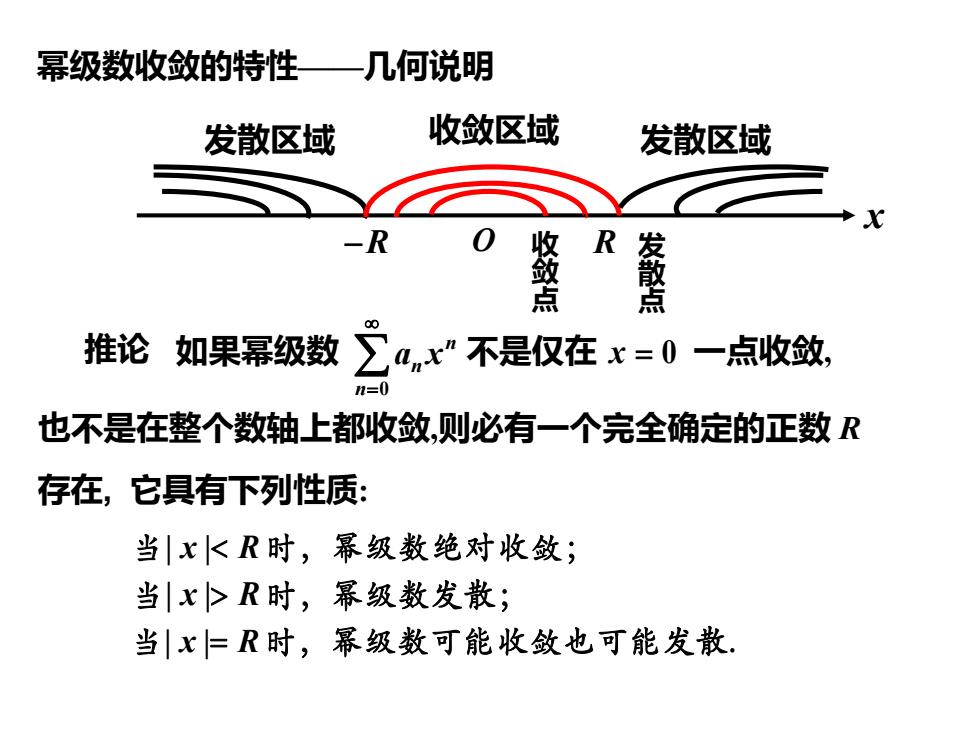
幂级数收敛的特性——几何说明 发散区域 收敛区域 发散区域 −R R x O 推论 0 n n n a x = 如果幂级数 不是仅在 x = 0 一点收敛, 存在, 它具有下列性质: 也不是在整个数轴上都收敛,则必有一个完全确定的正数 R 当| | x R 时,幂级数绝对收敛; 当| | x R 时,幂级数发散; 当| | x R = 时,幂级数可能收敛也可能发散. 收 敛 点 发 散 点

定义:正数R称为幂级数的收敛半径(-R,R)称为幂级数的收敛区间,收敛域=收敛区间+收敛的端点可能是(-R,R),[-R,R),(-R,R],[-R,R]规定(1)幂级数只在x=0处收敛时,R=0;(2)幂级数对一切x都收敛时,R=+0;问题:如何求幂级数的收敛半径?
( , ) −R R 称为幂级数的收敛区间, 收敛域 = 收敛区间 + 收敛的端点 可能是 ( , ), −R R [ , ), −R R ( , ], −R R 规定 R = 0; 问题: 如何求幂级数的收敛半径? 定义: 正数R 称为幂级数的收敛半径. [ , ]. −R R (1)幂级数只在x = 0处收敛时, (2)幂级数对一切 x 都收敛时, R = +;

8an+l定理2.若Zanxn的系数满足lim[=p,则ann-→n=01)当p时,R= O2)当p =0时,R= 80;3)当p =oo时,R=0.an+1+h+an+l证:lim= limoLXanxhn-00ann-一一1)若p0,则根据比值审敛法可知:当p|x<1,即|x<时,原级数收敛;当p|x|>1,即x[>时,原级数发散
x a a a x a x n n n n n n n n = + → + + → 1 1 1 lim lim 定理2. 若 的系数满足 ; 1 R = R = ; R = 0 . 证: 1) 若 ≠0, 则根据比值审敛法可知: 当 x 1 , 原级数收敛; 当 x 1 , 原级数发散. 即 1 x 时, 1) 当 ≠0 时, 2) 当 =0 时, 3) 当 =∞时, 即 时, 则 1 x 机动 目录 上页 下页 返回 结束