《线性代数》课程教学课件（讲稿，B）第四章 线性方程组 §4.3 非齐次线性方程组

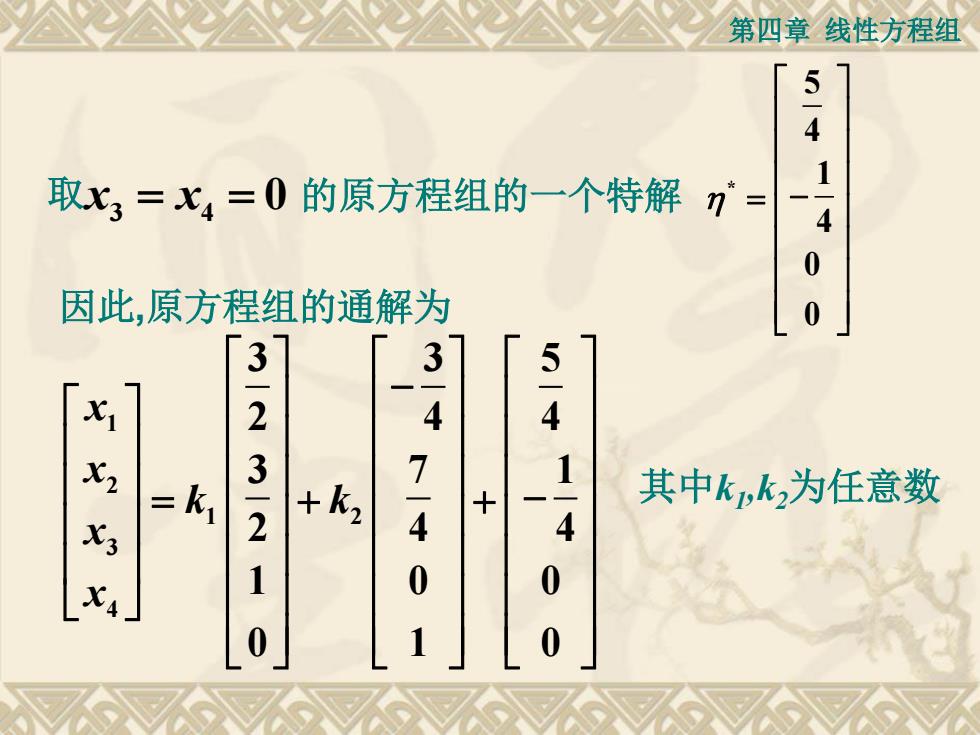
第四章线性方程组 5-4 取3=X4=0的原方程组的一个特解 1 n'= 0 因此，原方程组的通解为 0 3- 3 2 4 5-4 =k1 3-2 7-4 +k2 + 4 其中k,k,为任意数 1 0 0 0 0

第四章 线性方程组 取 3 4 x x = = 0 的原方程组的一个特解 * 5 4 1 4 0 0          = −           1 2 1 2 3 4 3 3 5 2 4 4 3 7 1 2 4 4 1 0 0 0 1 0 x x k k x x       −                         = + + −                                     因此,原方程组的通解为 其中k1 ,k2为任意数

第四章线性方程组 例2：求解方程组 x1-2x2+3x3-x4=1, 3x1-X2+5x3-3x4=2, 2X1+X2+2x3-2x4=3. 解：对增广矩阵进行初等行变换 1-23-11 53-3r「1-2 3-11 A= 3-15-3 2 05 -40-1 212-233-2r05-401

第四章 线性方程组 1 2 3 4 1 2 3 4 1 2 3 4 2 3 1, 3 5 3 2, 2 2 2 3. x x x x x x x x x x x x  − + − =   − + − =   + + − = 例2：求解方程组 1 2 3 1 1 3 1 5 3 2 2 1 2 2 3 A   − −   = − −       − 2 1 3 1 3 1 2 3 1 1 ~ 0 5 4 0 1 2 0 5 4 0 1 r r r r − − −     − −   − −     解： 对增广矩阵进行初等行变换

第四章线性方程组 1 -23 -1 1 一2 3 0 5 -4 0 -1 0 0 0 2 可见R(A)=2,R(A)=3,故原方程组无解

第四章 线性方程组 3 2 1 2 3 1 1 0 5 4 0 1 ~ 0 0 0 0 2 r r   − − −   − −       可见R A R A ( ) 2, ( ) 3, . = = 故原方程组无解