第6节 第三章 狐微多与曲率 曲线的弯 〔与切线的转角有关 曲程度 与曲线的弧长有关 M'M" 主要内容 一、弧微分 二、曲率及其计算 三、曲率圆 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 第6节 曲线的弯 曲程度 与切线的转角有关 与曲线的弧长有关 主要内容: 一、 弧微分 二、 曲率及其计算 三、 曲率圆 M M M 弧微分与曲率 第三章
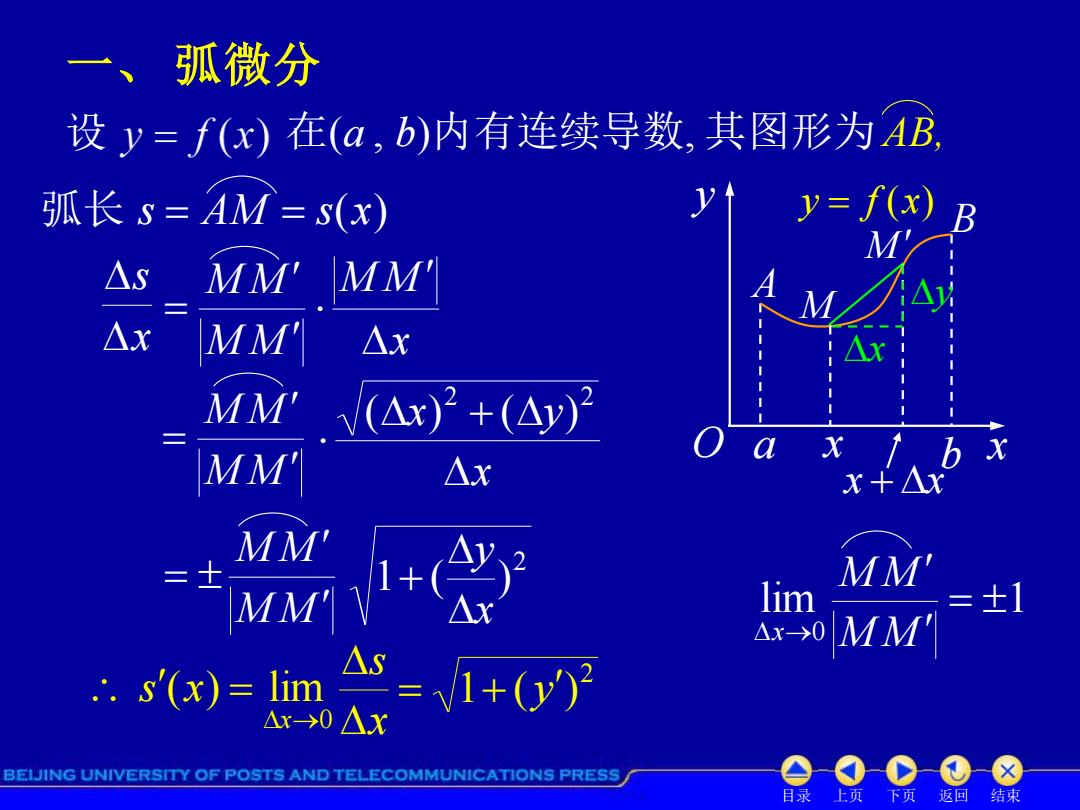
一、弧微分 设y=f(x)在(a,b)内有连续导数,其图形为AB 弧长s=AM=s(x) y=f(x) M △S MM'MM' △x MM' △x MM' V(△x)2+(△y)2 MM' a △x x i b x x+△X MM' = MM' lim =±1 Ax->0 MM' 's'()=tim= △x>0△X BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 一、 弧微分 设 在(a , b)内有连续导数, 其图形为 AB, 弧长 s AM s(x) x s M M M M x M M M M M M x x y 2 2 ( ) ( ) M M M M 2 1 ( ) x y x s s x x 0 ( ) lim 2 1 ( y ) x O y f (x) A B a b x y x M x x M y lim 1 0 M M M M x

s(x)=V1+(0y) .ds =+()2dx ds=v(dx)2+(dy)2 若曲线由参数方程表示: x=x(t) Ly=y(t) 永表示对 数t的导数 则弧长微分公式为 ds=V2+少2dt 几何意义:ds=MT dx cosa dy= sin a ds ds xx+dx x BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 下页 返回 结束
目录 上页 下页 返回 结束 则弧长微分公式为 ds x y d t 2 2 ds 1 ( y ) dx 2 或 2 2 ds (dx) (dy) O x dx dx x y x M dy T 几何意义: ds MT cos ; d d s x sin d d s y 若曲线由参数方程表示: ( ) ( ) y y t x x t 数 的导数 表示对参 t x

二、曲率及其计算 在光滑弧上自点M开始取弧段,其长为△s,对应切线 转角为△cx,定义 弧段△s上的平均曲率 K △ M △S 点M处的曲率 △0 da K lim △S ds 注意:直线上任意点处的曲率为0! BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 二、曲率及其计算 在光滑弧上自点 M 开始取弧段, 其长为 s , 对应切线 , 定义 弧段 s 上的平均曲率 s K M M s 点 M 处的曲率 s K s 0 lim ds d 注意: 直线上任意点处的曲率为 0 ! 转角为

例3.6.2求半径为R的圆上任一点处的曲率 解:如图所示 △S=R△C K=lim △0 △S R 可见:R愈小,则K愈大,圆弧弯曲得愈厉害; R愈大,则K愈小,圆弧弯曲得愈小 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页 下页返回 结束
目录 上页 下页 返回 结束 例3.6.2 求半径为R 的圆上任一点处的曲率 . 解: 如图所示 , s R s K s 0 lim R 1 可见: R 愈小, 则K 愈大 , 圆弧弯曲得愈厉害 ; R 愈大, 则K 愈小 , 圆弧弯曲得愈小 . s R M M