《高等数学》课程教学资源（课件讲稿）第一章_1.3.2-1.3.4

111例1 求 lim(2n2+222+1n→0Inn'+n11nn解Vn?n2+1+1+n+nnT又 limlim21n08+nn1 +n1nlimlim由夹逼定理得11n>+1n>心n111lim(22+2n-0+1n+nO高等数学（上册）

例1 ). 1 2 1 1 1 lim( 2 2 2 n n n n  n       求  解 , 1 1 1 1 2 2 2 2         n n n n n n n n   n n n n n n 1 1 1 lim 2 lim      又  1, 2 2 1 1 1 lim 1 lim n n n n n       1, 由夹逼定理得 ) 1. 1 2 1 1 1 lim( 2 2 2       n n  n n n 

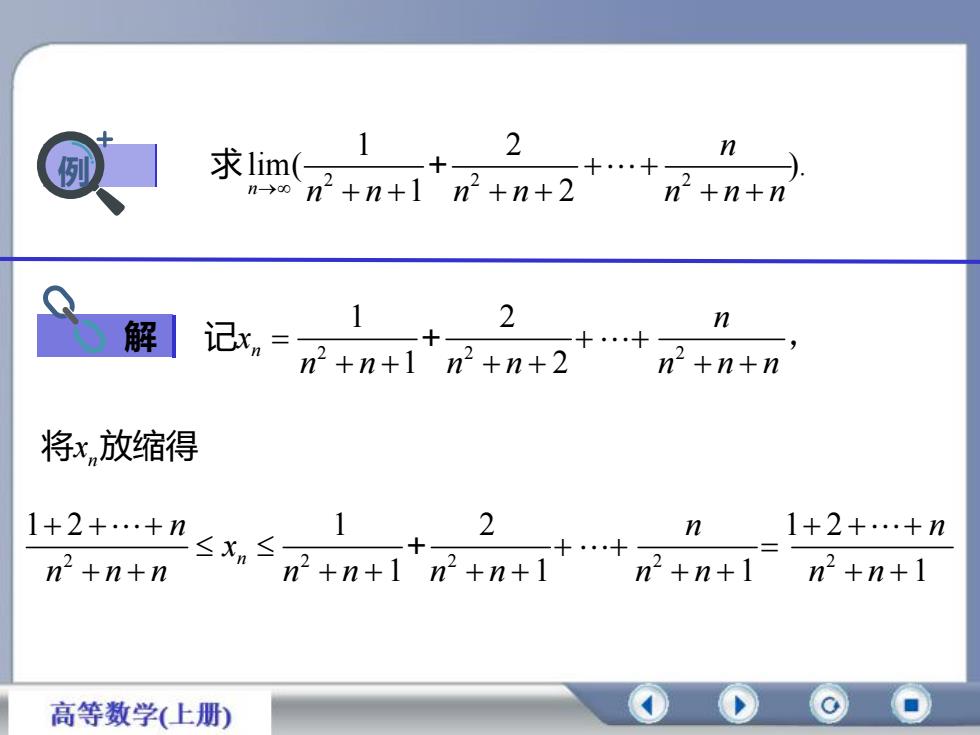
21n求lim(例.+n+2n>0+n+lnnn+n+nS21n角解记xn?+n+1n?+n+2n-+n+n将x,放缩得21+2+..+n1+2+...+nn≤x.<nn?+n+nn?+n+1-n+i+n+nn6高等数学（上册）

例 解 2 2 2 1 2 lim( ). n 1 2 n  n n n n n n n         求 ＋  2 2 2 1 2 1 2 n n x n n n n n n n          记 ＋  ， n 将x 放缩得 2 2 2 2 2 1 2 1 2 1 2 1 1 1 1 n n n n x n n n n n n n n n n n                        ＋ 

接n(n +1)11+2+...+n2而 limlim2'n?+n+n.n-00n>0n'+n+nn(n+ 1)11+2+...+n2limlimn2+n+1n-→ n? + n+12n-→001即根据夹逼准则得，limx2nn->021国nlim(2n?+n+2+n+1n→nn+n+nC高等数学（上册）

接 前 2 2 2 1 2 1 lim( )= . n 1 2 2 n  n n n n n n n         ＋  2 2 ( 1) 1 2 1 2 lim lim n n 2 n n n  n n n  n n n            而 ， 2 2 ( 1) 1 2 1 2 lim lim n 1 n 1 2 n n n  n n  n n            ， 1 lim = 2 n n x  根据夹逼准则得， ，即