由于不论常数C取何值。有积分曲线族[F(x)+C}' = f(x)同一x处其导数等于f(x),即y= F(x)+C各切线相互平行y= F(x)0x
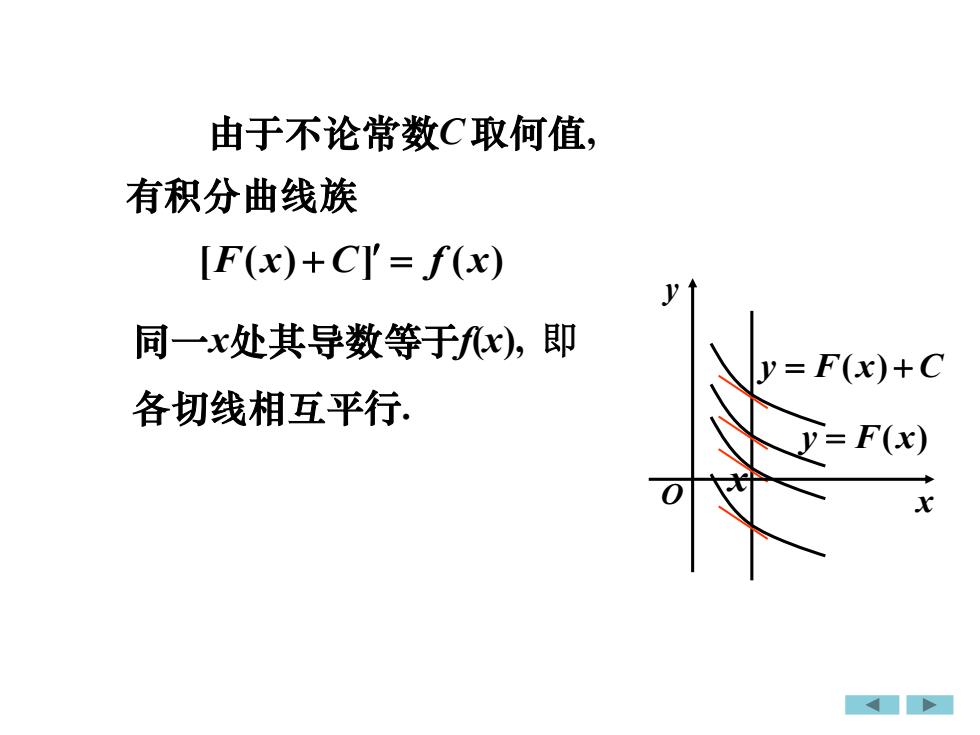
由于不论常数C 取何值, [F(x) + C] = f (x) 同一x处其导数等于f(x), 各切线相互平行. 有积分曲线族 即 x y = F(x) + C y = F(x) x y O
在求原函数的实际问题中,有时要从全部原函数中确定出所需要的具有某特性的一个原函数,这时应根据这个特性确定常数C的值,从而找出需要的原函数解J'=2x的曲线族为y= x2+2=[2xdx = 2 +Cy=x有 6=22+C =C=2故所求曲线方程为y = x2 + 2x
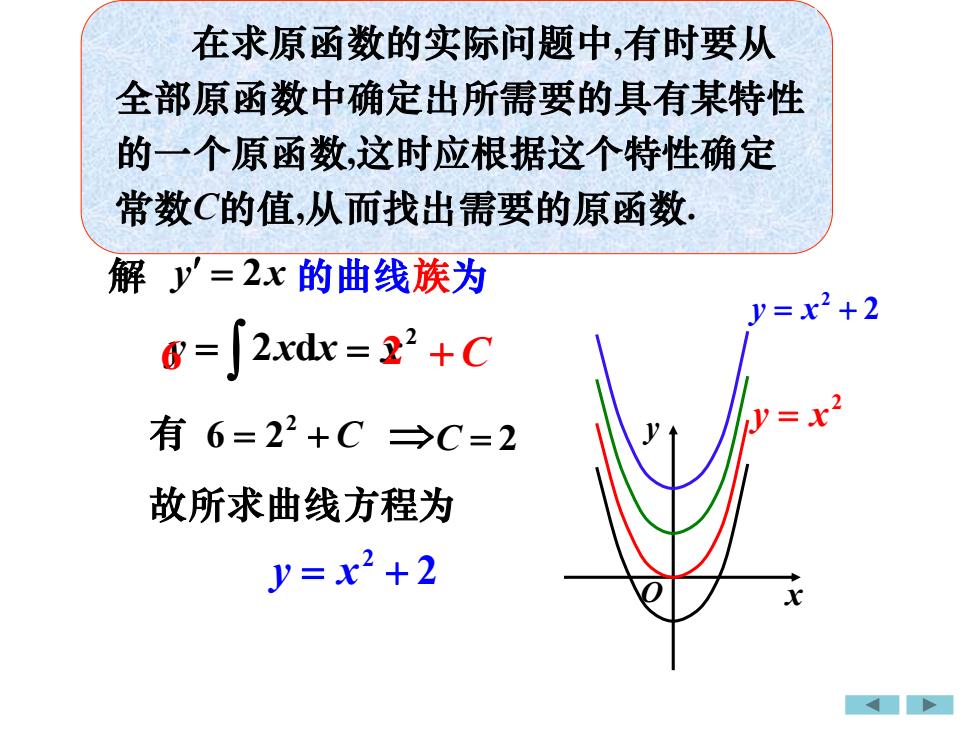
解 2 = x 故所求曲线方程为 2 2 y = x + (3) 积分常数的确定 例4 求通过点 (2,6), 且其切线斜率为2x曲线. 在求原函数的实际问题中,有时要从 全部原函数中确定出所需要的具有某特性 的一个原函数,这时应根据这个特性确定 常数C的值,从而找出需要的原函数. y = 2xdx y = 2x 的曲线族为 有 = + C 2 6 2 C = 2 6 2 + C 2 y = x 2 2 y = x + x y O