《高等数学》课程教学资源（PPT课件）第四章 不定积分 4-1 第四章 不定积分

定理如果F(αx)是f(x)在区间I上的一个原函数则(x)在区间I上的任一原函数都可表为F(x)+C 的形式,其中C为某一常数证 设G(x)为f(x)的另一个原函数,则G'(x) = f(x),要证F(x)-G(x)=常数又F'()= f(x),因为[G(x)- F(x)J = G'(x)-F'(x)= f(x)- f(x)= 0某个常数导数恒为零的函数必为常数故 F(x)-G(x) =C=>G(x) = F(x)+C只要找到f(x)的一个原函数，就知道它的全部原函数

故 0 F(x) − G(x) = C   =  G(x) − F(x) 0 G(x) = F(x) + C G( x) = f ( x), = f (x) − f (x)  证 设G(x)为f (x) 的另一个原函数,则 又 F( x) = f ( x),G(x) 只要找到f (x)的一个原函数,就知道 它的全部原函数. − F( x)  0 如果F(x)是f (x) 在区间I上的一个原函数, 则f(x)在区间I上的任一原函数都可表为 F(x) + C 其中C为某一常数. 定理 的形式, 要证 F(x) − G(x)  常数 因为 导数恒为零的函数必为常数 某个常数

总和(summa)2.不定积分(1) 定义定义2设F(x)是f(x)的任一原函数则f(x)的全部原函数的一般表达式 F(x)+C[.f(x)dx称为函数f(x)的不定积分.记为Q= F(x)+l积分常数被积表达式积分变量被积函数积分号

积 分 变 量 积 分 常 数 被 积 函 数 定义2 被 积 表 达 式 2. 不定积分 不定积分. (1) 定义 则f (x)的全部原函数的一般表达式 F(x) + C 称为函数f (x)的 总和(summa) f (x)dx 记为  积 分 号 f x x = F x + C  ( )d ( ) 设F(x)是f (x)的任一原函数

[f(x)dr=d[F(x)+C]1.被积函数是原函数的导数，被积表达式是原函数的微分2.不定积分表示那些导数等于被积函数的所有函数．或说其微分等于被积表达式的所有函数.因此绝不能漏写积分常数C3.求已知函数的原函数或不定积分的运算称为积分运算，它是微分运算的逆运算

=dF( x) + C   1. 被积函数是原函数的导数, 被积表达式是 原函数的微分.  f (x)dx 2. 不定积分表示那些导数等于被积函数的所 或说其微分等于被积表达式的所 有函数. 有函数. 因此绝不能漏写积分常数C. 3. 求已知函数的原函数或不定积分的运算称 为积分运算, 它是微分运算的逆运算

例2 求[x'dx.F(x)J解+C=x6dx.例3求1+xF(x)1解arctan x21+ xdx = arctan x +C

例2 求 d . 5 x x  解  =  x dx 5 解 例3 求 2 1 d . 1 x + x  ( ) =  F( x) C x + 6 6 2 1 1 + x  = +  x x d 1 1 2 arctan x arctan x +C ( ) 5 = x  6 6 x F( x)

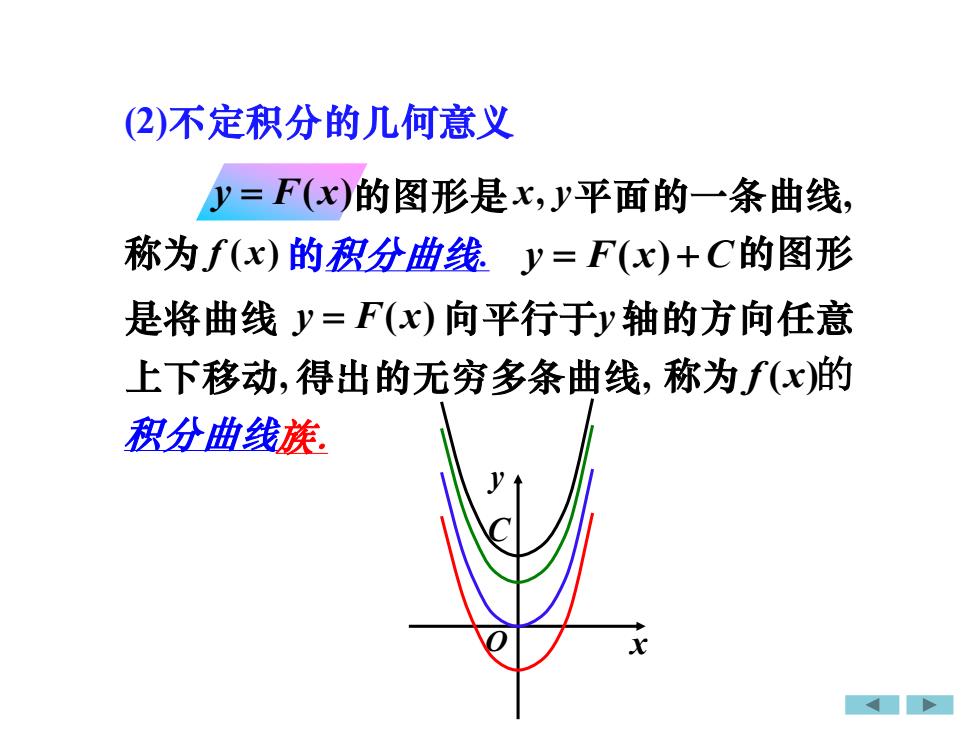
(2)不定积分的几何意义y=F(x)的图形是x,y平面的一条曲线称为f(x）的积分曲线y=F(x)+C的图形是将曲线 =F(x)向平行于y轴的方向任意上下移动,得出的无穷多条曲线，称为,f(x)的积分曲线族X

(2)不定积分的几何意义 积分曲线 y = F(x) 称为 f ( x) 的积分曲线. y = F(x) + C 的图形 y = F(x) 向平行于y 轴的方向任意 上下移动, 得出的无穷多条曲线, 称为 f (x)的 的图形是 x, y 平面的一条曲线, 是将曲线 族. x y O C