
线性代数第一节特征值与特征向量的概念与计算特征值与特征向量的定义目录特征值与特征向量的性质特征值与特征向量的计算思考题儿高事教商出成社1新时代大学数学东列教材
一 二 三 四 线性代数 第一节 特征值与特征向量的概念与计算 新时代大学数学系列教材 特征值与特征向量的定义 特征值与特征向量的性质 特征值与特征向量的计算 思考题
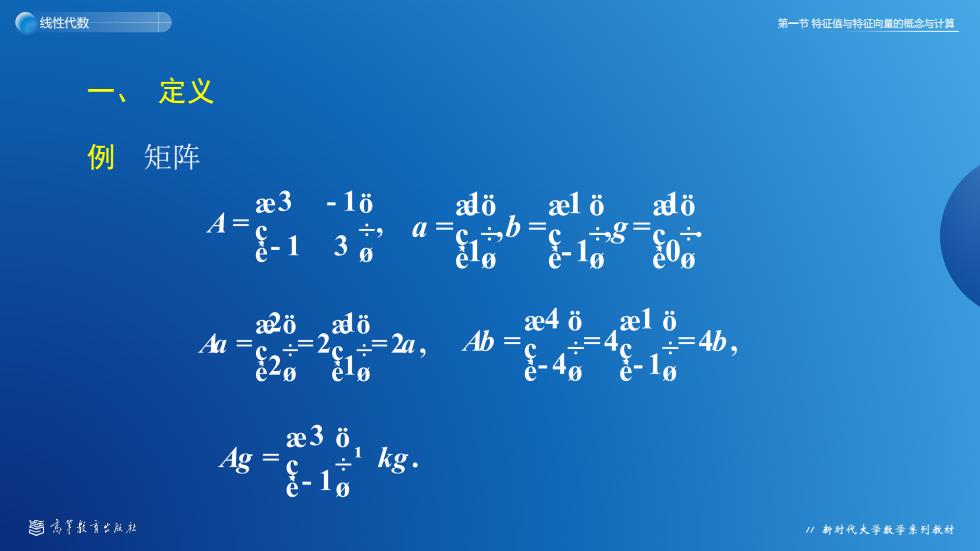
线性代数第一节特征值与特征向量的概念与计算一、定义例矩阵2e3-10adoael ado36A=2iga=$-1.1130002e40eloa20adoAb2=4b,2a,=Aa二分二=4C一?SS26-40e-10230kgAgX一6-10高教育出社11新时代大学数学系利教材
第一节 特征值与特征向量的概念与计算 新时代大学数学系列教材 线性代数 例 矩阵 一、 定义

线性代数第一节矩阵及其运算设Aip"",aip",liP定义若Aa=la (a1 0),则称1为A的一个特征值a为A对应于1的一个特征向量性质1.设Aa=la (a10),则A (ka )=k(Aa )=k(la)=l (ka)2. 设Aa,=l a; (i=1,2,L ,s),则A(ka,+ka, +L +ka,)=1 (ka,+ka, +L +ka,)高事教出服社新时代大学数学东列教材
第一节 矩阵及其运算 新时代大学数学系列教材 线性代数 定义 二、 性质

线性代数第一节特征值与特征向量的概念与计算特征子空间设V, =falAa=la,aiR"则由特征值与特征向量的性质可知"a,biV, a+biy"aiV,kiR,kaiy故V是n维向量空间R"的子空间V称为矩阵A的特征子空间思考:V的所有向量都是A的特征向量吗?首高事教育出服社1新时代大学数学系利教材
第一节 特征值与特征向量的概念与计算 新时代大学数学系列教材 线性代数 特征子空间

线性代数第一节矩阵及其运算三、计算设Aa=la(a10).则(-Aa=0α是(II-A)X=0的非零解求A的特征值与特征向量的步骤(1)求1-A=0的根:1,12,,(2)求(L,I-A)X=0的基础解系ayai,L,ai,则A对应于1的特征向量为:ka,+ka+L+k,ar(ki,kz,L,k,不全为零)首高事教育出服社11新时代大学数学系利教材
第一节 矩阵及其运算 新时代大学数学系列教材 线性代数 三、计算 求 A 的特征值与特征向量的步骤: