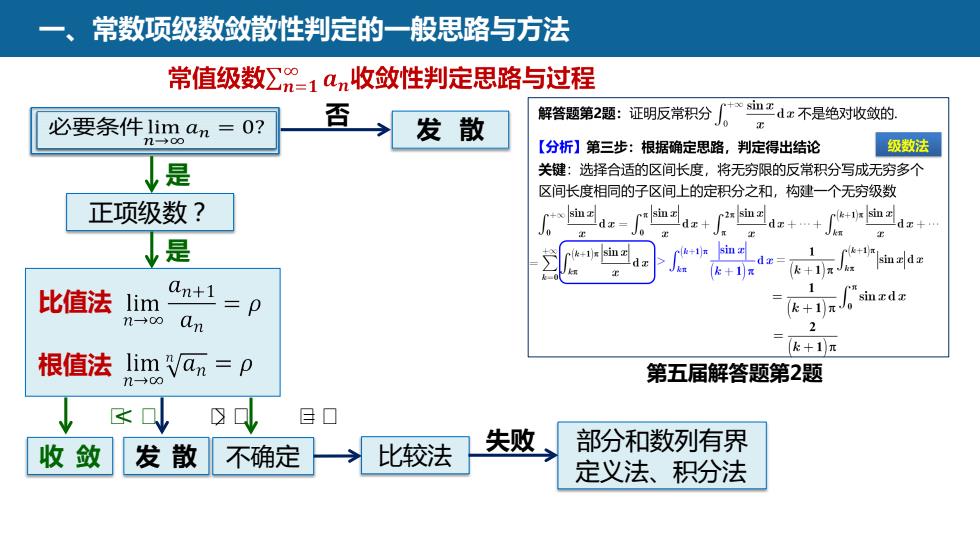
常数项级数敛散性判定的一般思路与方法常值级数Z=1an收敛性判定思路与过程sinda不是绝对收敛的否解答题第2题:证明反常积分必要条件liman=0?发散a0级数法【分析】第三步:根据确定思路,判定得出结论是关键:选择合适的区间长度,将无穷限的反常积分写成无穷多个区间长度相同的子区间上的定积分之和,构建一个无穷级数正项级数?sinzsinac2xsin2c(s+1)xsin ada+da+Jkna是sinae[k+1]n(k+1nk+1smzsinadada[k+1]元(k+1xJkan+1sinada比值法limO(k+1)元Jn-00an(k+1]元根值法lim"an=p第五届解答题第2题n-0口A口失败部分和数列有界比较法收敛发散不确定定义法、积分法
一、常数项级数敛散性判定的一般思路与方法 否 收 敛 比较法 正项级数? 发 散 是 是 比值法 根值法 ᵼ< ᵼ 发 散 ᵼ> ᵼ 不确定 ᵼ= ᵼ 失败 部分和数列有界 定义法、积分法 第五届解答题第2题
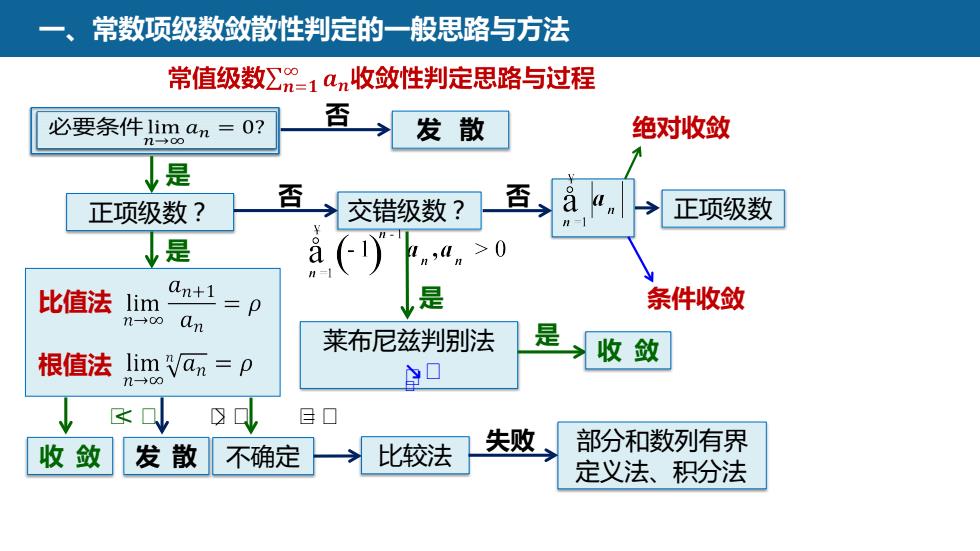
常数项级数敛散性判定的一般思路与方法常值级数Z=1an收敛性判定思路与过程否必要条件liman=0?绝对收敛发散n是否否ae正项级数交错级数?正项级数?+oa()是>0,aan+1是条件收敛比值法lim二pn-00an是莱布尼兹判别法收敛根值法lim"an=pn-0口贝口失败部分和数列有界收敛比较法发散不确定定义法、积分法
一、常数项级数敛散性判定的一般思路与方法 否 收 敛 比较法 正项级数? 发 散 是 是 比值法 根值法 ᵼ< ᵼ 发 散 ᵼ> ᵼ 不确定 ᵼ= ᵼ 失败 部分和数列有界 定义法、积分法 否 交错级数? 是 莱布尼兹判别法 是 收 敛 否 正项级数 绝对收敛 条件收敛 ᵼᵼ ↘ᵼ

常数项级数敛散性判定的一般思路与方法练习题1:设f(α)是在(a,+o)(α >0)单调递增且大于0的连续函数,an单调递增X1aX收敛d&收敛,则级数且大于零,证明:若>af(ac)aan=1【提示) f(x)> 0 f(x)z ;α,> 0anz:0-Bons11aa(a)ta)a-1吉f (anf (aa.n++11an+ 11an+1dxtdx00an+yf (an+i)xf(x)aanan+1aN+1E8oaFdxdx00xf(x)xf(x)(11an1=1
一、常数项级数敛散性判定的一般思路与方法 【提示】