
能事伦与散理统计」 第六章数理统计的基本概念 创关键词: 总体 个体 样本 统计量 X2-分布 t-分布 下分布
第六章 数理统计的基本概念 关键词: 总 体 个 体 样 本 统 计 量 2 −分布 t −分布 F −分布

概華论与款醒硫外「 1.总体与样本 ·总体:研究对象的全体 ·抽样:从总体X中抽取有限个个体对总体进行 观察的取值过程。 ·随机样本:随机抽取的n个个体的集合 (X1,X2,.,X),n为样本容量 X以) 1.每个X与X同分布 4w) 2.X1,X2,.,Xn是相互独立的随机变量
1.总体与样本 • 总体:研究对象的全体 • 抽样:从总体X中抽取有限个个体对总体进行 观察的取值过程。 • 随机样本:随机抽取的n个个体的集合 (X1,X2,.,Xn), n为样本容量 1. 每个Xi与X同分布 2. X1,X2,.,Xn是相互独立的随机变量

概车纶与款理统外 2.抽样分布 ·统计量:样本的不含任何未知参数的函数。 ·常用统计量:设(X1,X2,.,X)为取自总体X的样本 1样本均值又=2名 2样本方老S-十2X-X.5为样本标准养 3.样本矩 4空r低2及56 阶中心矩:B=2(X-X(k=12,) 设X1,X2,X是总体X的样本,若E(X)=4,DX)=o2, X=4D五=g,S)=a
2.抽样分布 • 统计量:样本的不含任何未知参数的函数。 • 常用统计量:设(X1,X2,.,Xn)为取自总体X的样本 1 1 1. X n i i X n = 样本均值 = 2 2 1 1 2. ( ) , 1 n i i S X X S n = = − 样本方差 − 为样本标准差 ( ) ( ) 1 1 1 3. 1,2, 1 ( ) 1,2, n k k i i n k k i i k A X k n k B X X k n = = = = = − = 样本矩 阶矩: 阶中心矩: 2 2 2 2 2 , ,., ( ) , ( ) ( ) , ( ) , ( ) . X X X E X D X n E X D X E S n = = = = = 设 1 X 是总体 的样本,若 , 则
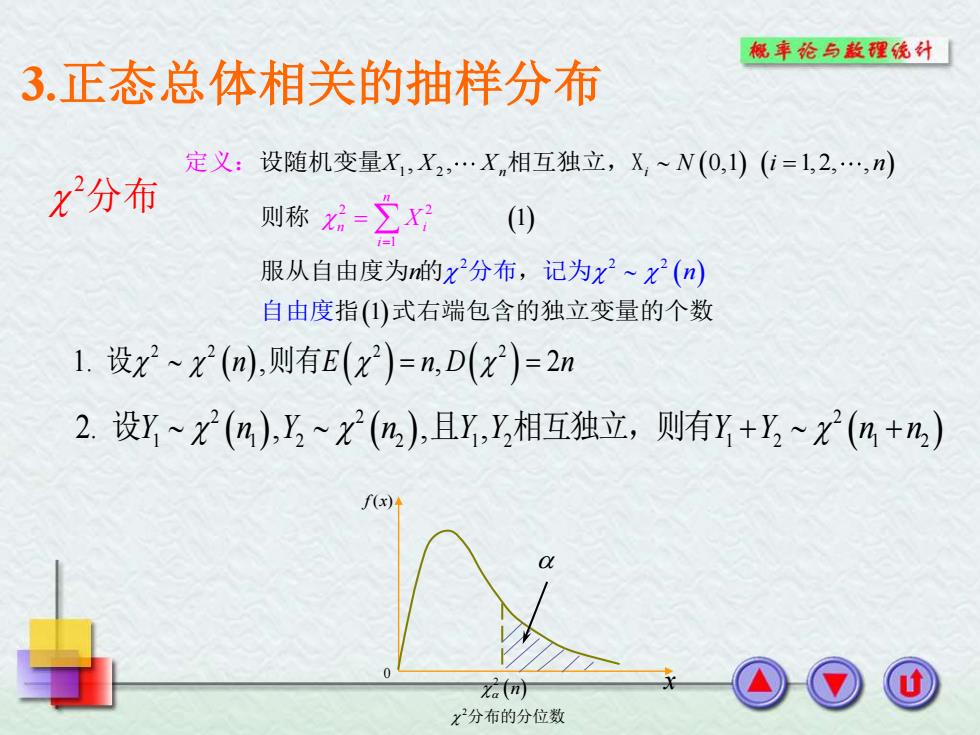
概率伦与款程统外 3.正态总体相关的抽样分布 定义:设随机变量X,X2,.Xn相互独立,X,~(0,1)(位=1,2,.,n) x分布 则称-立X () 服从自由度为n的x2分布,记为x2~x2(n) 自由度指()式右端包含的独立变量的个数 1.设x2~X2(n),则有E(x2)=n,D(x2)=2n 2.设r~X(n),出,~X(h),且X,相互独立,则有y+~X(n+n) f(x)4 xa(寸 x分布的分位数
3.正态总体相关的抽样分布 2 分布 ( ) ( ) ( ) ( ) ( ) 1 2 2 2 2 2 2 1 , , 0,1 1, 2, , 1 1 n i n i n i X X X N i X n n n = = = 设随机变量 相互独立,X 则称 服从自由度为 的 , 定 指 式右端包含 分布 记为 自 度 的独立变 义: 由 量的个数 ( ) ( ) ( ) 2 2 2 2 1. , , 2 设 = = n E n D n 则有 ( ) ( ) ( ) 2 2 2 1 1 2 2 1 2 1 2 1 2 2. , , , 设Y n Y n Y Y Y Y n n + + 且 相互独立,则有 ( ) 2 n 0 2 分布的分位数 x f x( )
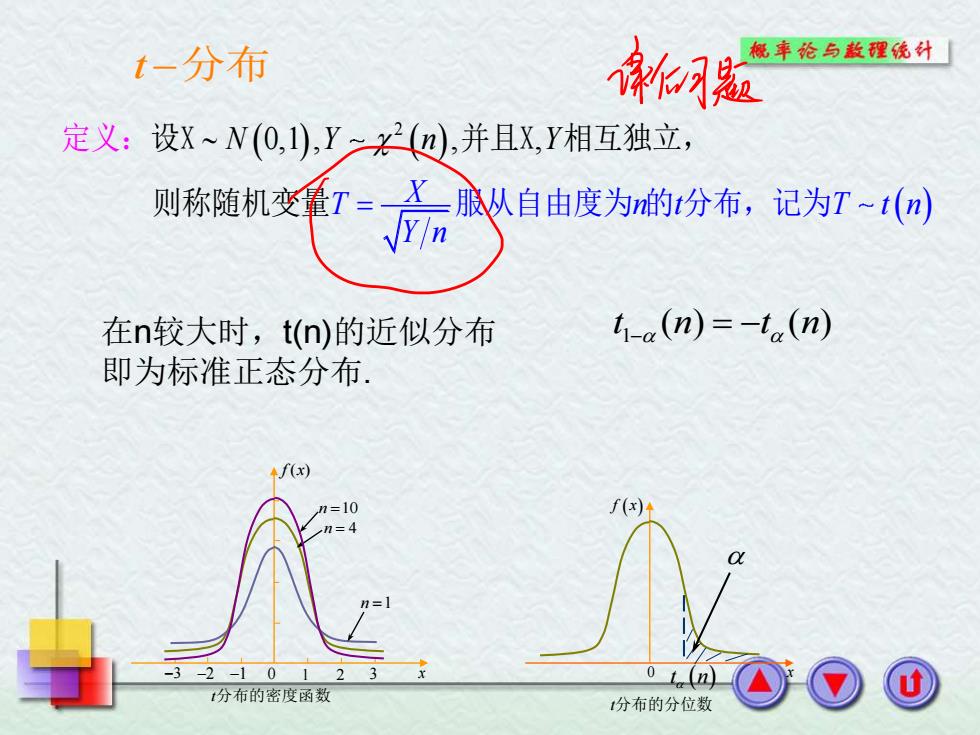
t-分布 概车纶与散理统外「 定义:设x~N(0,1),Y一(,并且X,Y相互独立, 则称随机变看T=X服从自由度为的分布,记为T-1(n) 在n较大时,t(n)的近似分布 t-a(n)=-ta (n) 即为标准正态分布! (x) () -3-2-1012 o t (n 1分布的密度函数 分布的分位数
t −分布( ) ( ) ( ) 2 N Y n 0,1 , , , X T n t T t Y n Y n = 设X 并且X 相互独立, 则称随机变量 服从自由度为 的 分布,记为 定义: t n ( ) f x( ) 0 x t分布的分位数 n =10 −3 1 3 x f x( ) n =1 n = 4 −2 −1 0 2 t分布的密度函数 1 t n t n ( ) ( ) 在n较大时,t(n)的近似分布 − = − 即为标准正态分布