概率伦与款程统外 来F分布 N.七 #定义:设X~x2(n),Y~x2(n2),且X,Y独立, 则称随机变量F X1m服从自由度(n,n)的F分布,记为F-F(m,) YIn 其中n,称为第一自由度,n,称为第二自由度 性质 F~F(nn),F(nn) F-a(n,n2)=[E(n2,n)]f f(x) f(x) 乃=0,4=20 25 =10 0 Fa(n,n) F分布的密度函数 F分布的分位数
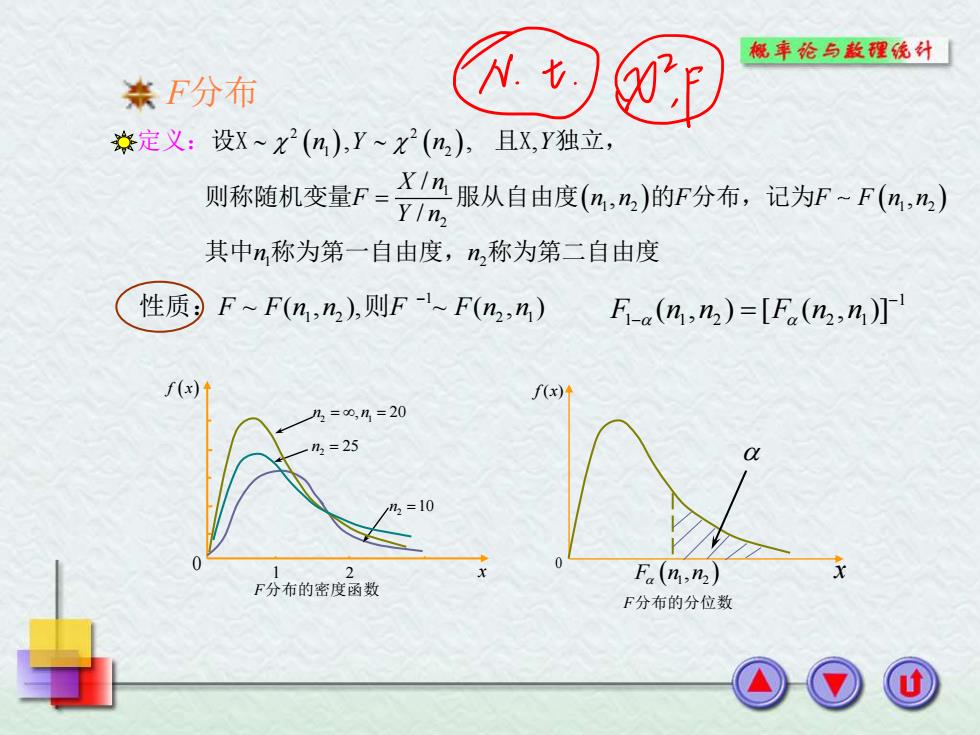
( ) ( ) ( ) ( ) 2 2 1 2 1 1 2 1 2 2 1 2 , , , / , , / n Y n Y X n F n n F F F n n Y n n n = 设X 且X 独立, 则称随机变量 服 定义: 从自由度 的 分布,记为 其中 称为第一自由度, 称为第二自由度 F分布 1 F F n n F F n n ~ ( , ), ~ ( , ) 1 2 2 1 性质: 则 − 0 1 2 x f x( ) 2 1 n n = = , 20 2 n = 25 2 n =10 F分布的密度函数 0 ( ) x 1 2 F n n, f x( ) F分布的分位数 1 1 1 2 2 1 F n n F n n ( , ) [ ( , )] − − =

正态总体样本均值和方差的分希 定理66:设(X,X,奶总体N(uo)的样本,S 分别是样本均值和样本方差,则有: 2 (n-1)s2 (n-1 灭nw(u,a) 3.灭和S相互独立 定理67:设(X,.,X是总体N(4,o2)的样本,x和S2分别是样本 均值和样本方差,则有:- SIn
正态总体样本均值和方差的分布 ( ) ( ) ( ) ( ) ( ) 2 2 2 1 2 2 2 2 2 , , , , , 1. X , - 1 2. 1 3. 6.6 n n X X X N X S N n S n X S − 设 是总体 的样本, 分别是样本均值和样本方差 定理 : ,则有: 和 相互独立 ( ) ( ) ( ) ( ) 2 2 1 . , , , 1 / 6 7 X X N S n X t n S n − − 设 是总体 的样本,X和 分别是样本 均值和样本方差,则有: 定理 :