
概车纶与款理统外 第二章 随机变量及其分布 习题课 一、重点与难点 二、主要内容 三、典型例题
一、重点与难点 二、主要内容 三、典型例题 第二章 随机变量及其分布 习 题 课

概率伦与款理统外 一、重点与难点 1.重点 (0-1)分布、二项分布和泊松分布的分布律 正态分布、均匀分布和指数分布的密度函数 及有关概率的计算 2.难点 随机变量的分布函数的求法 连续型随机变量的函数的分布
一、重点与难点 1.重点 (0-1)分布、二项分布和泊松分布的分布律 正态分布、均匀分布和指数分布的密度函数 及有关概率的计算 2.难点 随机变量的分布函数的求法 连续型随机变量的函数的分布
概车纶与款理统外 二、主要内容 密度 函 数 分布函数 布律 连续型 离散型 随机变量 随机变量 随机变量 均匀分布 指教分布 正态分布 随机变量 定 的函数的 点分布 项 习 分布 布 松分布
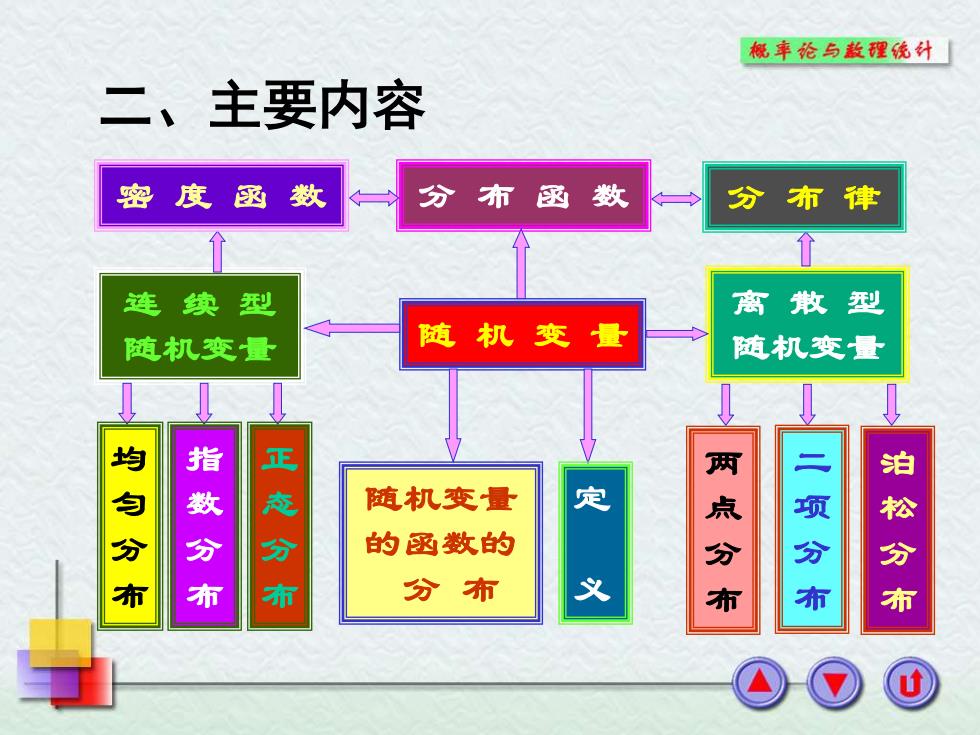
二、主要内容 随 机 变 量 离 散 型 随机变量 连 续 型 随机变量 密 度 函 数 分 布 函 数 分 布 律 均 匀 分 布 指 数 分 布 正 态 分 布 两 点 分 布 二 项 分 布 泊 松 分 布 随机变量 的函数的 分 布 定 义

概華论与款醒硫外 随机变量 定义设E是随机试验,它的样本空间是S={}.如 果对于每一个eeS,有一个实数X(e)与之对应,这 样就得到一个定义在S上的单值实值函数X(),称 随机变量. ()随机变量与普通的函数不同 (2)随机变量的取值具有一定的概率规律 (3)随机变量与随机事件的关系
. ( ), , ( ) , , { }. 随机变量 样就得到一个定义在 上的单值实值函数 称 果对于每一个 有一个实数 与之对应 这 定义 设 是随机试验 它的样本空间是 如 S X e e S X e E S e = (1)随机变量与普通的函数不同 随机变量 (2)随机变量的取值具有一定的概率规律 (3)随机变量与随机事件的关系

概车纶与款理统外 随机变量的分类 随机变量 离散型 非离散型 连续型 其它 随机变量所取的可能值是有限多个或无限 可列个,叫做离散型随机变量
随机变量的分类 离散型 随机变量 连续型 非离散型 其它 随机变量所取的可能值是有限多个或无限 可列个, 叫做离散型随机变量