《高等数学》课程教学资源（PPT课件）第四章 不定积分 4-2 第二节 换元积分法

小结( f(sin x)cos xdx = ( f(sin x)dsinx[ f(cos x)sin xdx = - f(cos x)dcosxf f(tanx)sec'xdx =f f(tanx)dtanxJ f(cotx)csc'xdx =-J f(cot x)dcot x1[ f(arcsin x)Jf (arcsinx)darcsinx[ f(arctanx) ( f(arctanx)darctanxYrdf(x)=In,f(x) + Cf(x)f(x)

小结 =  f (tanx)sec xdx 2 =  f (cot x)csc xdx 2 = +  x x f x d 1 1 (arctan ) 2  f (sin x)cos xdx =  f (cos x)sin xdx =  f (sin x)dsinx  − f (cos x)dcosx  f (tanx)dtan x  − f (cot x)dcot x  f (arctanx)darctanx = −  x x f x d 1 1 (arcsin ) 2 f (arcsin x)darcsin x = ln f (x) + C  ( ) d ( ) f x f x =   x f x f x d ( ) ( )

[ f(tan x)sec'xdx = J f(tan x)d tan x练习dx1.17cos x(1 + tan x)1+ tan xIn1 + tan x+ C1 + tan x3/x2313/xX13/x2dxd/xe3Vx2/3V+CO3J (Vx)= 2J (Vx)d(/x)

 cos (1+ tan ) d 1. 2 x x x  + + = x x 1 tan d(1 tan ) d 3  = x e d(3 ) 3 2 3 e x x  x = x e x 2. d 3  e C x = + 3 3 2   f (tan x)sec xdx = f (tan x)dtan x 2 = ln 1+ tan x + C 2 x =  x x f x d ( ) 2 f ( x)d( x) 

arctanx + C例4 求arctan=+Caa011解X20x001xax1+a01Xarctan=+Caa

例4 求 x a x d 1  2 2 + 解 x a x d 1  2 2 + x a a x d 1 1 1 2 2 2  + = x a a x d 1 1 1 2  2       + = C a x a = arctan + 1 x a x d 1  2 2 + C a x a = arctan + 1 = +  x x d 1 1 2 arctan x +C             + =  a x a a x d 1 1 1 2

x=arctan=+Cdr:0aa1dx例5 求x28x+2511解dxY2(x -4)2 +92-8x+251d(x - 4)32 +(x- 4(x - 4)71x-4+Carctan33

例5 求 x x x d 8 25 1  2 − + 解 x x x d 8 25 1  2 − + x x d ( 4) 9 1  2 − + = C x + − = 3 4 arctan 3 1 x a x d 1  2 2 + C a x a = arctan + 1  + − − = 2 2 3 ( 4) d( 4) x x x x d 3 ( 4) 1  2 2 + − =

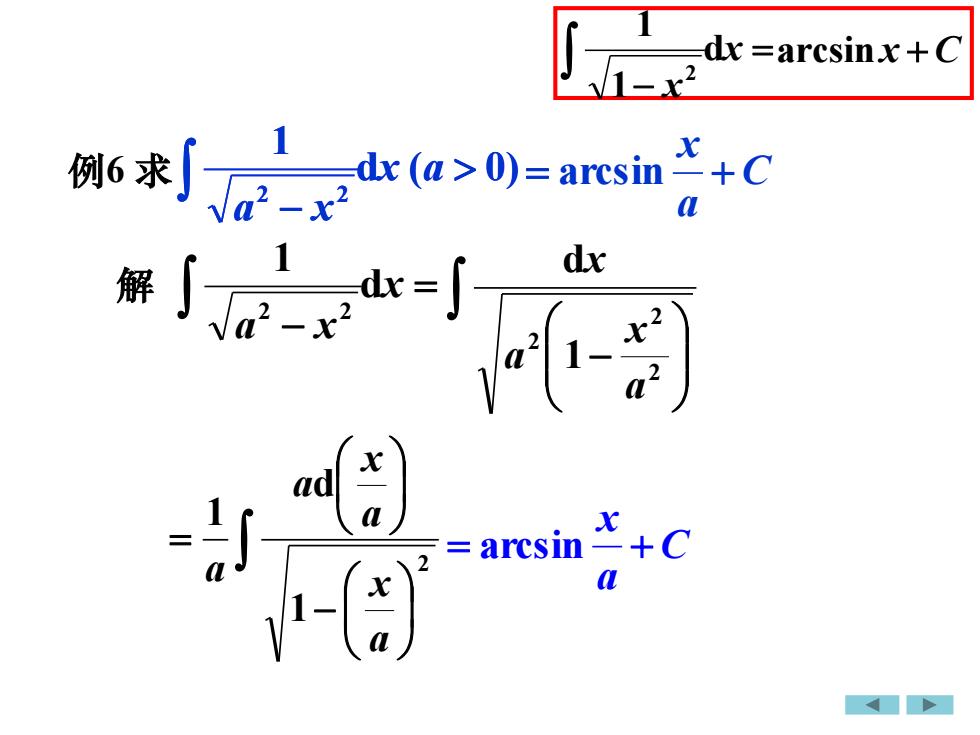
dx =arcsinx + C例6 求dx (a > 0)= arcsin -=+C2adx解adaarcsin-+Ca

例6 求 解 = −  x a x d 1 2 2        −       = 2 1 d 1 a x a x a a C a x = arcsin + d ( 0) 1 2 2  −  x a a x = −  x x d 1 1 2 arcsin x +C d ( 0) 1 2 2  −  x a a x C a x = arcsin +          − 2 2 2 1 d a x a x