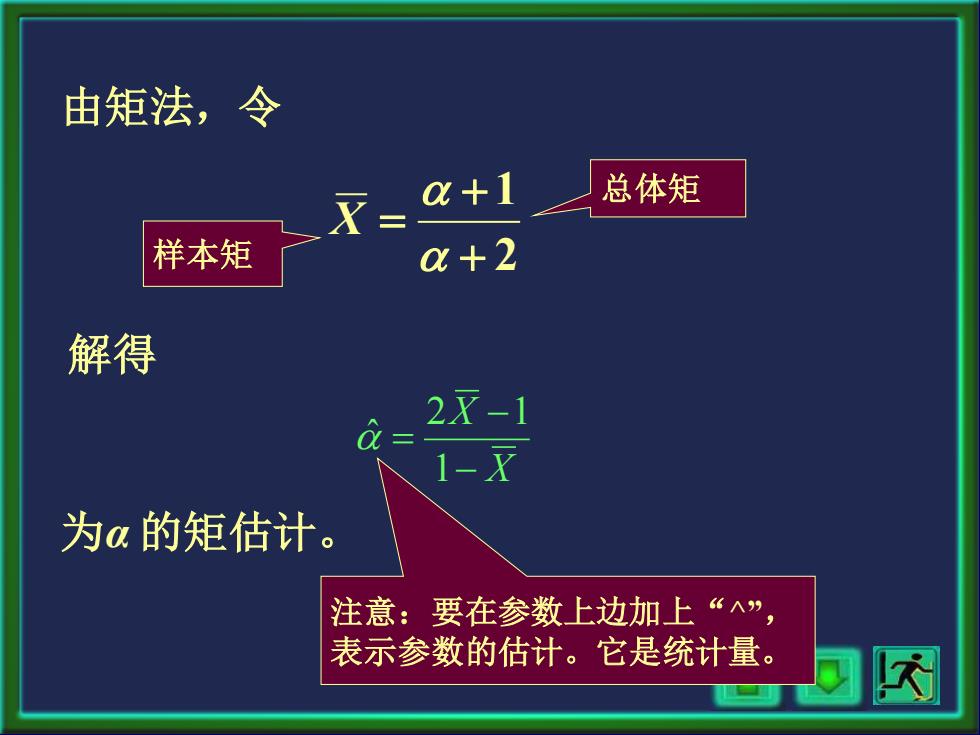
由矩法,令 a+1 总体矩 样本矩 a+2 解得 2x-1 1-X 为a的矩估计。 注意:要在参数上边加上“”, 表示参数的估计。它是统计量。 网
由矩法,令 2 1 + + = X 样本矩 总体矩 解得 X X − − = 1 2 1 ˆ 为α 的矩估计。 注意:要在参数上边加上“^” , 表示参数的估计。它是统计量

例2:设X1X2,.Xn是取自总体X的简单样本, X有概率密度函数 (x-4)/0 e x24, 其他 其中0,u为未知参数,0>0。求0,u的矩估计。 解:先求总体的均值和2阶原点矩。 X0=合ewd =0y+u)edy =0+4 @四的
解: 先求总体的均值和2阶原点矩。 例2:设X1 ,X2 , .Xn 是取自总体X的简单样本, X 有概率密度函数 其 中 为未知参数, 。求 的矩估计。 其 他 , 0 , 0, . , , 1 ( ) ( ) = − − e x f x x E X x e x x d 1 ( ) ( ) − − = 令y=(x-μ )/θ θ y e y y ( ) d 0 − = + = θ +

令y=(x4)/0 =(0y+}'e'dy =(02y2+20uy+2)e'dy =202+20u+u =02+(0+4)2, @@风
E X x e x x d 1 ( ) 2 2 ( ) − − = 令y=(x-μ )/θ ( ) , 2 2 ( 2 ) d ( ) d 2 2 2 2 0 2 2 2 0 2 = + + = + + = = + + = + − − θ θ θ θ y y e y θ y e y y y

u+0= 0+u-r-2x9 用样本矩 估计总体矩 得 6-三-x2x- 2=x-空-对 立,日为参数山,0的矩估计. a四
用样本矩 估计总体矩 ˆ, ˆ为参数 , 的矩估计。 + + = + = =ni Xi nX 1 2 2 2. 1 ( ) , 令 得 = − − = − = − = = = ( ) . 1 ˆ ( ) , 1 1 ˆ 1 2 1 2 1 2 2 ni i ni i ni i X X n X X X n X nX n

例3:设总体X的均值为4,方差为o,求和 o的矩估计。 a(4,o)=E(X)=4, 解:由 a(u,o2)=E(X2)=o2+42 4(4,o2)=, 列出方程组: auo)=≥x 4=X, 即 。2+h=2x @@网
列出方程组: = = + = = ( , ) ( ) . ( , ) ( ) , 2 2 2 2 2 2 1 a E X a E X = = = . 1 ( , ) ( , ) , 1 2 2 2 2 1 n i Xi n a a X + = = = n i Xi n X 1 2 2 2 . 1 , 即 例3:设总体X的均值为,方差为 2 ,求和 2 的矩估计。 解:由