
例1.验证方程siny+e-xT-1=0在点0,0)谋邻域 可确定一个单值可导隐函数1=f().并求 出 dxx=0 解:令F(.)=simy-e-xy-1,则 ①F=e-F,=cosy-x连续, ②F(0.0)=0. ③F(0.0)=1≠0 由定理1可知,在x=0的某邻域内方程存在单值可 导的隐函数1=(x).且 HIGH EDUCATION PRESS 机动目 下页返回结
例1. 验证方程 在点(0,0)某邻域 可确定一个单值可导隐函数 解: 令 连续 , 由 定理1 可知, ① 导的隐函数 则 ② ③ 在 x = 0 的某邻域内方程存在单值可 且 机动 目录 上页 下页 返回 结束 并求

=0 Er=0- e"-T cos 1'-A d dr- X=0 d dr cos-r下=0.y=0.'=-1 (e-')c0s-)-(e-1)-sin1‘-l) 1=0 (C0s1'-x) 7 -3 HIGH EDUCATION PRESS 机动目录上页下页返回结束
机动 目录 上页 下页 返回 结束
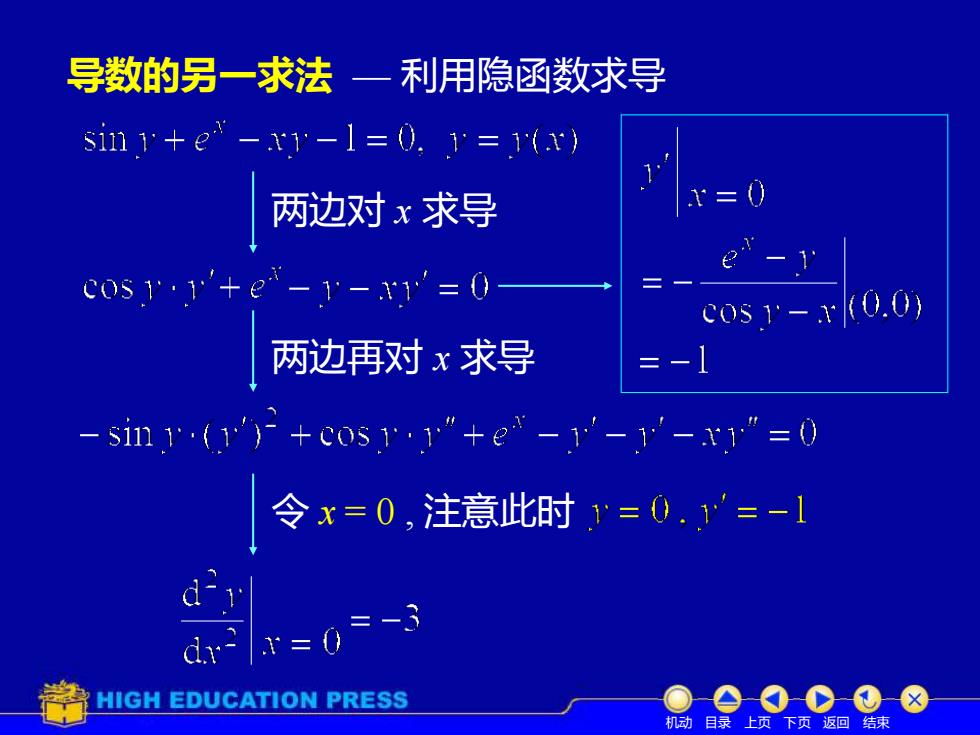
导数的另一求法一 利用隐函数求导 sin1+e-x-1=0.1=1(r) 两边对x求导 x=0 e"-1 c0s1'+e-Y-x1'=0 c0s1-x(0.0) 两边再对x求导 =-1 in1(')+e0s.1“+e-1-3'-x”=0 令x=0,注意此时y=0.=-1 d-r d2x=0=-3 HIGH EDUCATION PRESS 机动目录上页下页返回结束
两边对 x 求导 两边再对 x 求导 令 x = 0 , 注意此时 导数的另一求法 — 利用隐函数求导 机动 目录 上页 下页 返回 结束

定理2.若函数F(x.)满足 ①在点P(x0.0.-)的某邻域内具有连续偏导数, ②F(0.10.6)=0 ③F(0.0,-o)≠0 则方程F(x.)=0在点(x0)某一邻域内可唯一确 定一个单值连续函数z=f(x,y),满足三0=/0·10). 并有连续偏导数 3= Fs. F 定理证明从略,仅就求导公式推导如下 HIGH EDUCATION PRESS 机动目录上页下页返回结束
定理2 . 若函数 的某邻域内具有连续偏导数 , 则方程 在点 并有连续偏导数 定一个单值连续函数 z = f (x , y) , 定理证明从略, 仅就求导公式推导如下: 满足 ① 在点 满足: ② ③ 某一邻域内可唯一确 机动 目录 上页 下页 返回 结束

设:=f(x.)是方程F(my)=0所扉定的隐函数.则 F(x.f(3x.1))≡0 两边对x求偏导 Fx+F: 在(xo,0a)的某减内F=0 F 同样可得 F HIGH EDUCATION PRESS 机动目录上页下页返回结束
两边对 x 求偏导 同样可得 则 机动 目录 上页 下页 返回 结束