
一般周期序列的DFS表示(周期为M)N-!SW(t-1)mx[K]=[,[-[1-0m=0K[wwNZ1=0Wi定义:x[1]WlmX[m]=AIX[m]Wmkx[K] =N2对周期为N的任意周期序列N-l+nZx[k]X[K] =2k=<N>k=0k=nX[m]=DFS([K] = Z [KJWm"x[K]= IDFS(X[m]) =X[mjW-7A<N例:x[K]=2cos(元k/5),试求其10点的DFS系数。(10exp(j2元k/10)+10exp(-j2元k/10)x[k]=-101(10W+10W)10 -1≤m≤8范围内X[m|=10, m=-1,1X[m]=0,其他0≤m≤9范围内X[m]=10, m=1,9X[m]=0,,其他
一般周期序列的 DFS 表示(周期为 N) 定义: 对周期为 N 的任意周期序列 例:x[k]=2cos( k/5), 试求其 10 点的 DFS 系数。 [ ] ~ [ ] ~ 1 1 0 x k x k N n k n N k − + = − = = [ ] ~ [ ] ~ [ ] ~ 1 0 x k x l k l N N l = − − = k l m N N m N l x l W N ( ) 1 0 1 0 [ ] 1 ~ − − − = − = = km N lm N N l N m x l W W N − − = − = = [ ] 1 ~ 1 0 1 0 lm N N l X[m] ~x[l]W ~ 1 0 − = = mk N N m X m W N x k − − = = [ ] 1 ~ [ ] ~ 1 0 = = k N x[k] ~ mk N k N X[m] DFS{ ~x[k]} ~x[k]W ~ = = = mk N m N X m W N x k X m − = = = [ ] 1 ~ [ ]} ~ [ ] IDFS{ ~ {10exp( 2 /10) 10exp( 2 /10)} 10 1 [ ] ~x k = j k + − j k {10 10 } 10 1 10 10 k k W W − = + −1 m 8范围内 [ ] 10, 1,1 ~ X m = m = − [ ] 0, 其他 ~ X m = 0 m 9范围内 [ ] 10, 1,9 ~ X m = m = [ ] 0, 其他 ~ X m =
例:求如图所示周期方波序列的DFS系数N>2M+1AX[m)=-DFS(x[k=Z x[kw -2。当m=0.±N,±2N...时有X[m]=2M+1对m的其它取值,利用等比级数的求和公式有Tm14m(M+1)X[m]msin-NN=30,M=2周期方波的DFS系数N=30,M-12周期方波的F[m] DFS系数10010设N是一奇数,则由部分DFS系数确定的时域信号的部分和为之 X[m]expx,[K]=-kmAx,[k]0.5521010N=13,M=3,p=1的部分和
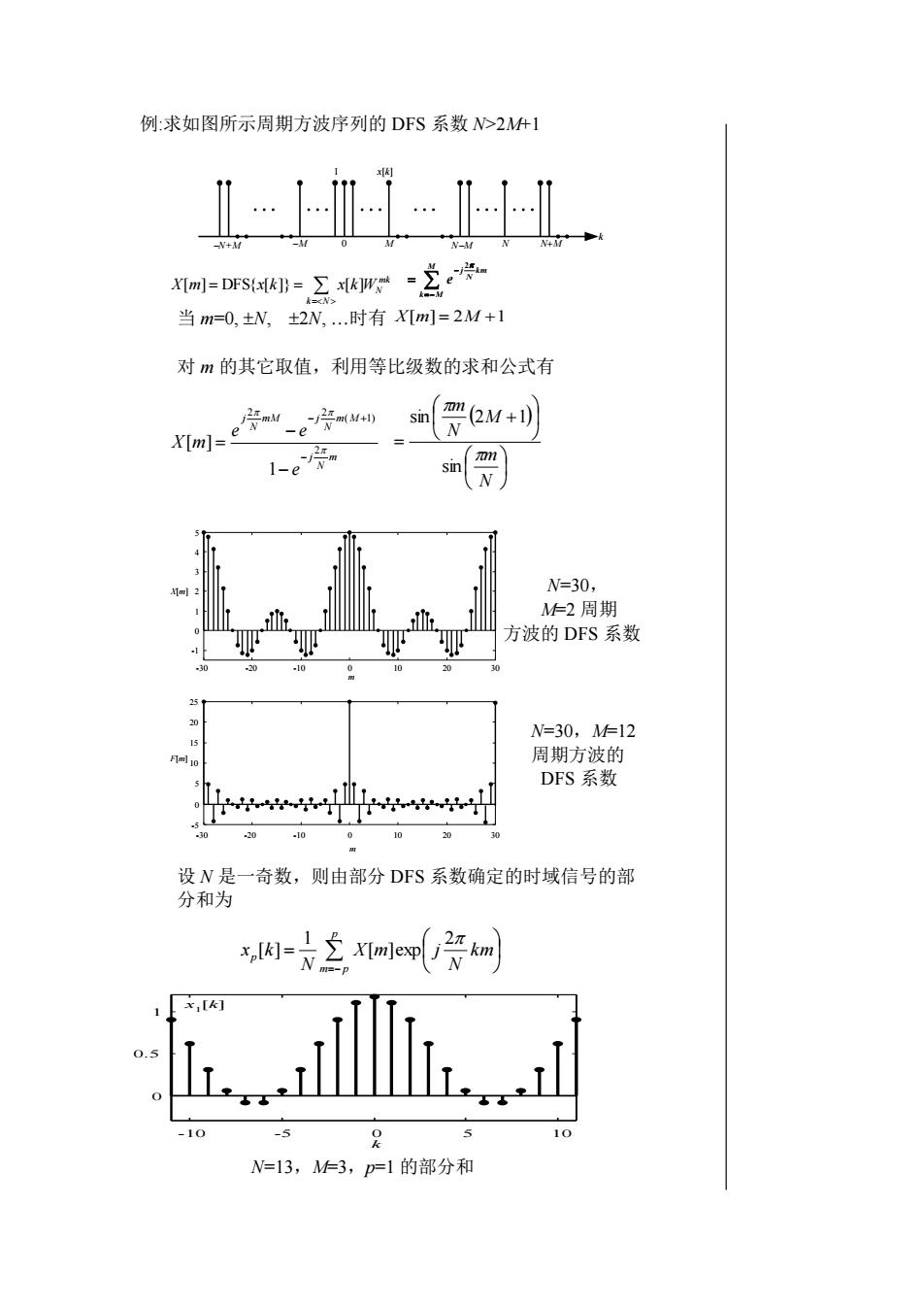
例:求如图所示周期方波序列的 DFS 系数 N>2M+1 当 m=0, N, 2N, 时有 对 m 的其它取值,利用等比级数的求和公式有 N=30, M=2 周期 方波的 DFS 系数 N=30,M=12 周期方波的 DFS 系数 设 N 是一奇数,则由部分 DFS 系数确定的时域信号的部 分和为 N=13,M=3,p=1 的部分和 M k 1 0 x[k] −N+M −M N−M N N+M mk N k N X[m] DFS{x[k]} x[k]W = = = km N j M k M e 2 − =− = X[m] = 2M +1 m N j m M N mM j N j e e e X m 2 ( 1) 2 2 1 [ ] − − + − − = ( ) + = N m M N m sin sin 2 1 -30 -20 -10 0 10 20 30 -1 0 1 2 3 4 5 m X[m] -30 -20 -10 0 10 20 30 -5 0 5 10 15 20 25 m F[m] = =− km N X m j N x k p m p p 2 [ ]exp 1 [ ] -10 -5 0 5 10 0 0.5 1 x 1 [k] k
x-[k]-10010N=13,M=3kp=2的部分和x[k]0.5OK51010-5N=13,M=3,p=3的部分和x[k]0.4..05-10-510N=13,M=3,p=4的部分和xs[k]0.5-10-50310kN=13,M=3,p=5的部分和xe[k]0.5-55-10210N=13,M=3,p=6的部分和
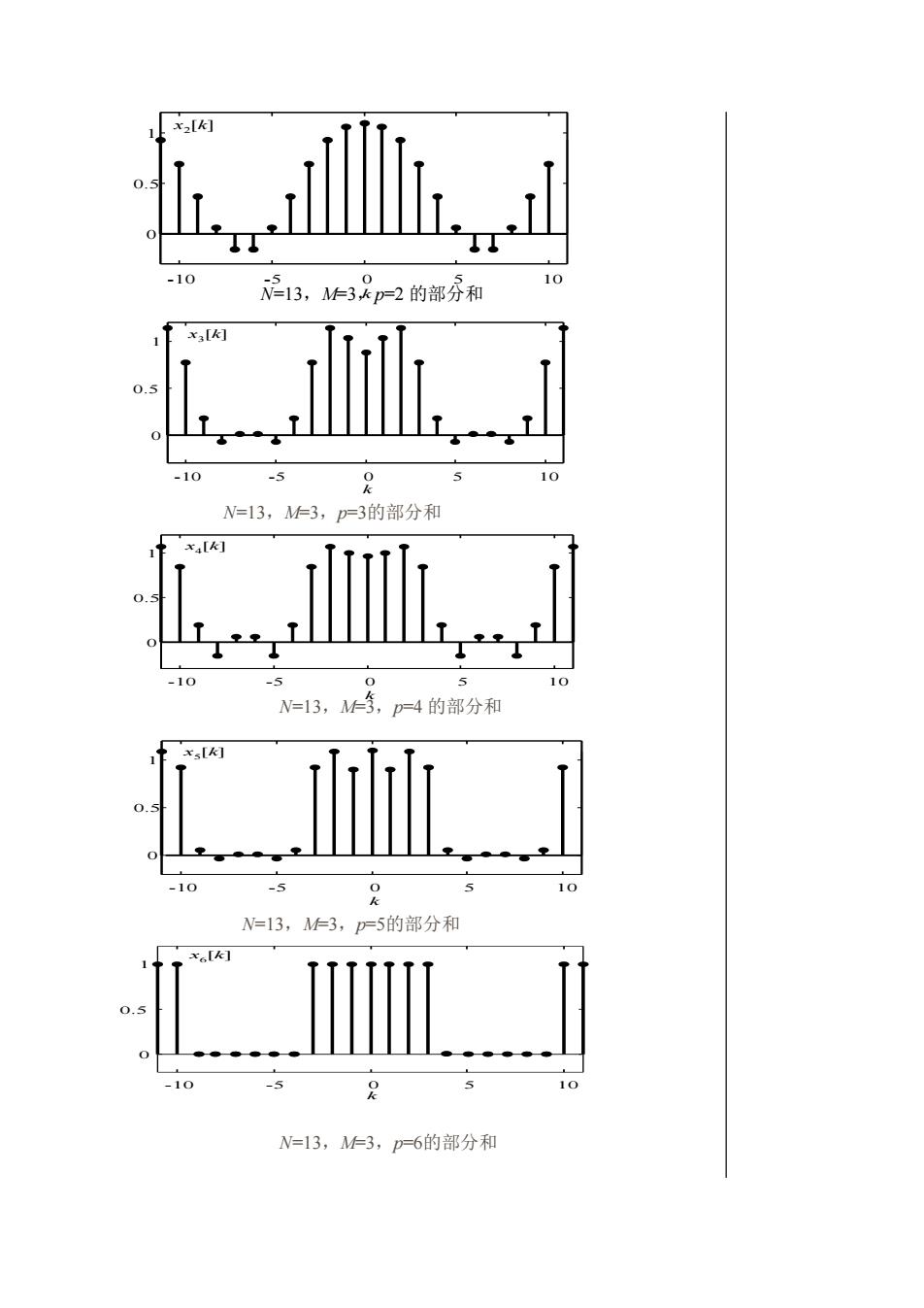
N=13,M=3,p=2 的部分和 N=13,M=3,p=3的部分和 N=13,M=3,p=4 的部分和 N=13,M=3,p=5的部分和 N=13,M=3,p=6的部分和 -10 -5 0 5 10 0 0.5 1 k x2 [k] -10 -5 0 5 10 0 0.5 1 k x3 [k] -10 -5 0 5 10 0 0.5 1 k x5 [k] -10 -5 0 5 10 0 0.5 1 k x4 [k] -10 -5 0 5 10 0 0.5 1 k x 6 [k]
1.3.2DFS的基本性质1.线性DFS(ax,[K]+bx,[K]}=aDFS([K]) +bDFS([k]2.位移[K]43x[k + 2]K0123a)时域位移DFS(x[k +n]} =W-"" X[m]b)频域位移DFS(Wlkx[k])=X[m+1]证:DFS([k+n] =x[k+n]Wmkk=<N>+儿 x[r]W(c-m)=CN>=W"Z x[r]w"r=<N>=W-" X[m]3.对称性DFS(*[k]} =X*[-m]DFS[(*[-]} =X*[m]
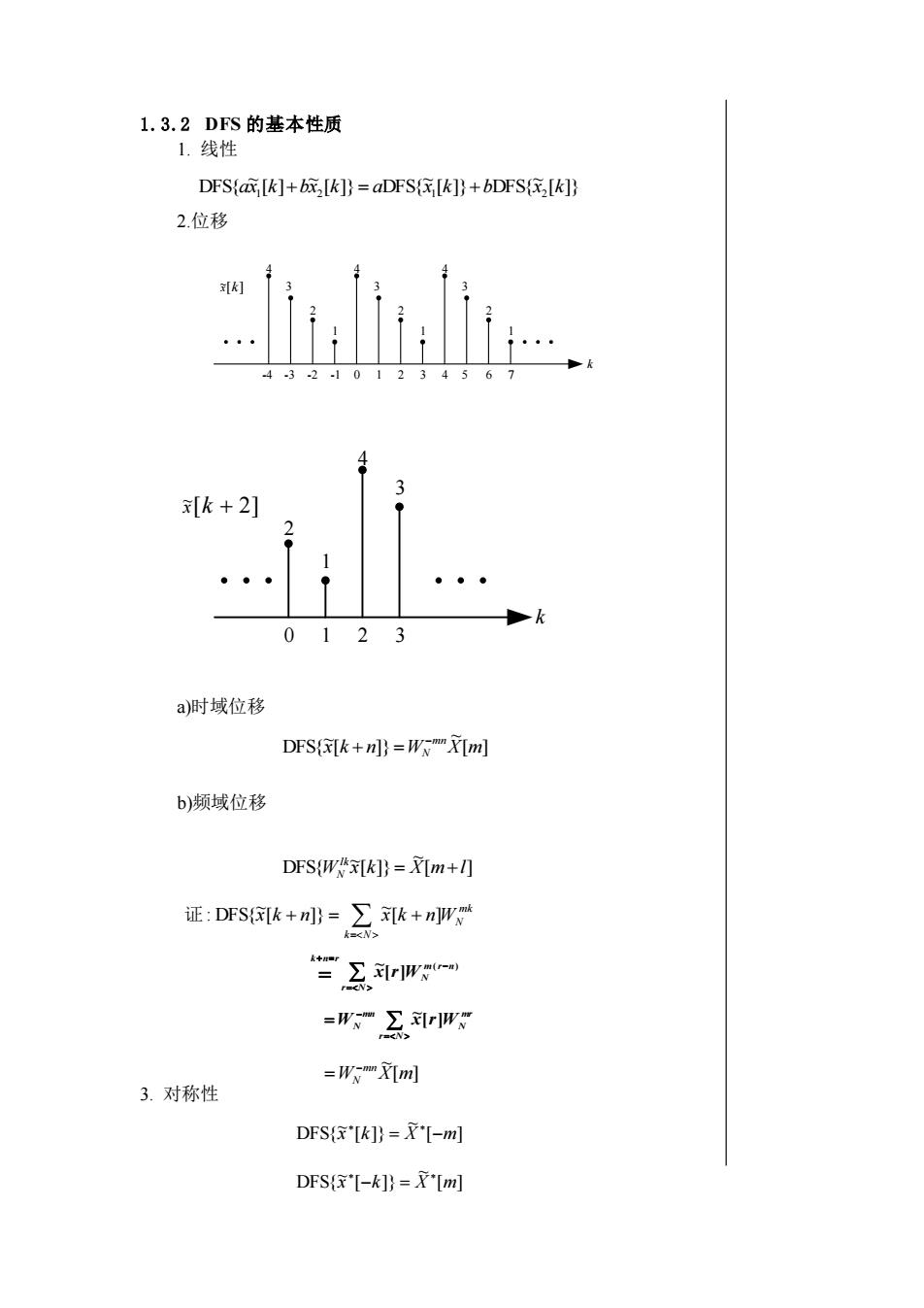
1.3.2 DFS 的基本性质 1. 线性 2.位移 a)时域位移 b)频域位移 3. 对称性 0 1 2 3 k [ 2] ~ x k + 4 3 2 1 [ ]} ~ [ ]} DFS{ ~ [ ]} DFS{ ~ [ ] ~ DFS{ 1 2 1 2 ax k +bx k = a x k +b x k 0 1 2 3 k -4 -3 -2 -1 4 5 6 7 [ ] ~x k 4 3 2 1 4 3 2 1 4 3 2 1 [ ] ~ [ ]} ~ DFS{x k n W X m mn N − + = [ ] ~ [ ]} ~ DFS{W x k X m l lk N = + mk N k N : DFS{ ~x[k + n]} = ~x[k + n]W = 证 ( ) [ ] ~ m r n N r N k n r x r W − = + = = mr N r N mn WN x ~ [r]W = − = [ ] ~ W X m mn N − = [ ] ~ [ ]} ~ DFS{x k = X −m [ ] ~ [ ]} ~ DFS{x k X m − =
周期序列的对称偶对称x[k]=x[-k]=x[N - k]N=5N=440实序列X[m]= X[-m]偶对称实序列X[m]实偶对称DFS(x[k]}=X'[-m]DFS(x[-k]}=X*[m]奇对称x[Kk]=-x[-k]=-x[N-k]N=4N=53K012奇对称实序列X[m]=-X'[m]实部为零,虚部奇对称4.周期卷积定理定义:(周期卷积)N-[K][K]-x[n]x[k-nn=0例:已知周期N=3的序列,如图所示,试计算Y[k]= x[k]* x[k]
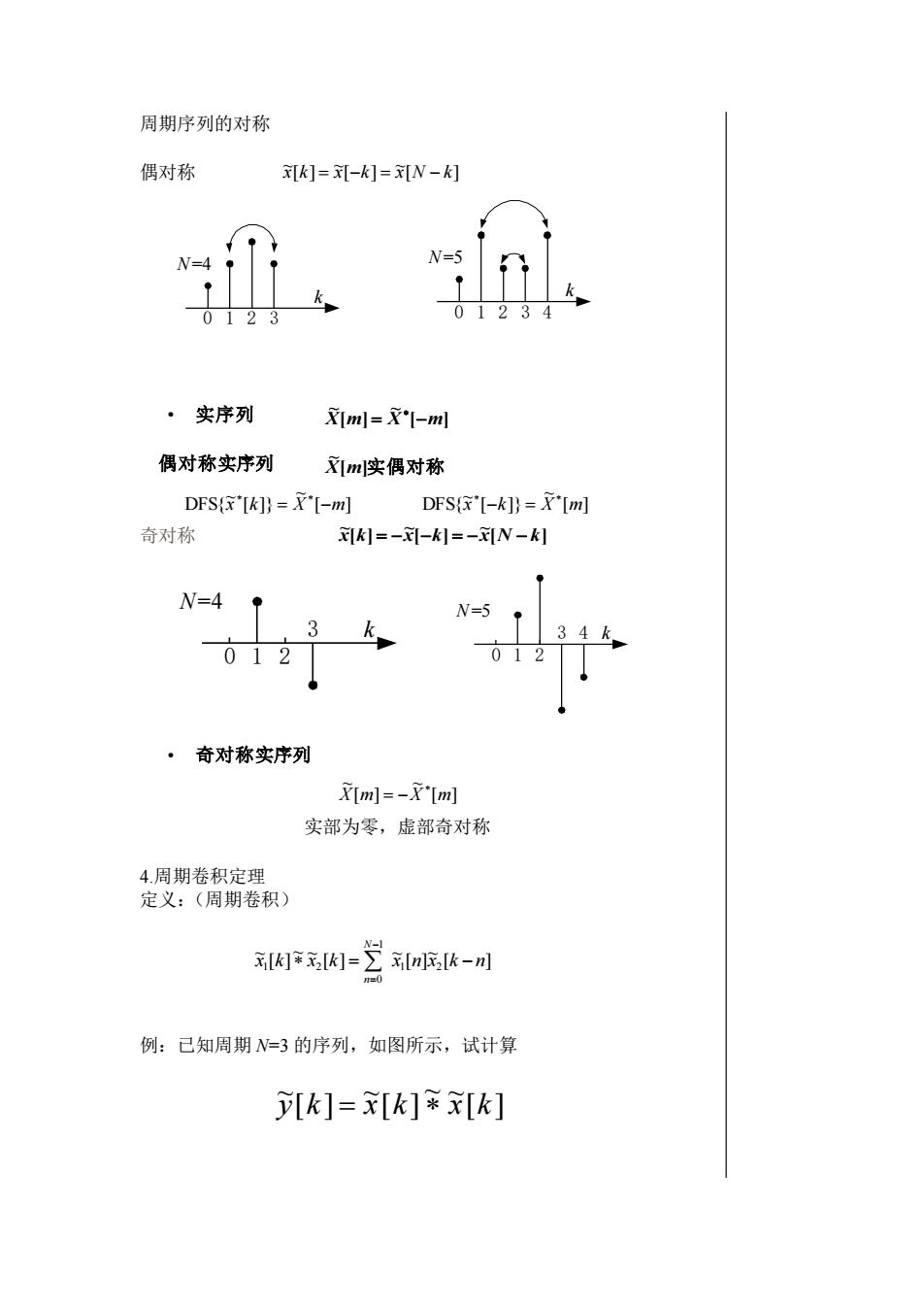
周期序列的对称 偶对称 • 实序列 偶对称实序列 奇对称 • 奇对称实序列 实部为零,虚部奇对称 4.周期卷积定理 定义:(周期卷积) 例:已知周期 N=3 的序列,如图所示,试计算 [ ] ~ ~ [ ] ~ [ ] ~ y k = x k x k [ ] ~ [ ] ~ [ ] ~ x k = x −k = x N − k 0 1 2 3 k N=4 0 1 2 3 k N=5 4 [ ] ~ [ ] ~ X m = X −m [ ]实偶对称 ~ X m [ ] ~ [ ]} ~ DFS{x k = X −m [ ] ~ [ ]} ~ DFS{x k X m − = [ ] ~ [ ] ~ [ ] ~ x k = −x −k = −x N − k 0 1 2 3 k N=4 0 1 2 4 k N=5 3 [ ] ~ [ ] ~ X m X m = − [ ] ~ [ ] ~ [ ] ~ ~ [ ] ~ 1 2 1 0 x1 k x2 k x n x k n N n = − − =