
x,[k]kRk012342345抽取器时变特性的图示说明3.因果性(Causality)定义:系统k时刻的输出只和k时刻及以前的输入有关。因果的 LTI:h[k]=0k<0.例:Mi+M+1点滑动平均系统定义为艺+川1>[Kk]=M,+M,+1,-求和范围k-M,k+M,A当M2=0时,系统是因果的。(1(M,+M,+1) -M,≤k≤Mh[k]=其它0
抽取器时变特性的图示说明 3.因果性(Causality) 定义:系统 k 时刻的输出只和 k 时刻及以前 的输入有关。 因果的 LTI:h[k]=0, k<0. 例:M1+M2+1 点滑动平均系统定义为 当 M2=0 时,系统是因果的。 1 2 3 4 5 2 6 4 k 0 [ ] 1 x k -1 1 3 5 1 2 3 4 5 k -1 0 1 3 5 1 2 3 4 5 2 6 4 k -1 0 1 3 5 1 2 3 4 5 2 6 4 k -1 0 1 2 3 4 5 2 6 4 k -1 0 1 3 5 1 2 3 4 k -1 0 1 3 5 [ ] 1 1 [ ] 2 1 2 1 x k n M M y k M n M + + + = =− k k M1 k − M 2 k + 求和范围 + + − = 0 其它 1/( 1) [ ] 1 2 2 M1 M M M k h k

4.稳定性定义(B.I.B.O)当输入,如输出满足,则称系统是稳定的。定理:LTI系统稳定的充分必要条件是Z[[k] = S<8k=-证:1.充分性[[]=[n[k-n]≤Z[n][k-n]≤M,Z[k-n]=M,Z[n]n2.必要性[h*[-k]/|[-k] [-k]+0x[k]=10h[-k]=0[0]=x[n]h[-n] =h*[-n][-n]/[-n] =-Z[n[-n]|= S例:(MI+M2+1点滑动平均)C[[k]=]1.2.2离散LTI系统的响应及性质1.单位脉冲响应(Impulseresponse)定义:h[k] = To[k]例:累加器:[k]=x[n]n=-h[k] = u[k]2.LTI系统对任意输入的响应T(x[k]) = T(x[n][k-n]]x[n]T(o[k-n]x[n][k-n]
4.稳定性 定义(B.I.B.O) 当输入, 如输出满足,则称系统是稳定的。 ●定理:LTI 系统稳定的充分必要条件是 证:1.充分性 2.必要性 例:(M1+M2+1 点滑动平均) 1.2.2 离散 LTI 系统的响应及性质 1. 单位脉冲响应(Impulse response) 定义: 例:累加器: 2. LTI 系统对任意输入的响应 h[k ] = u[k ] = k =− h[k] S = − n y[k] x[n]h[k n] x[n] h[k n] n − M h[k n] n x − M h[n] n = x − = − − − = 0 [ ] 0 *[ ]/ [ ] [ ] 0 [ ] h k h k h k h k x k = − n y[0] x[n]h[ n] = − − − n h*[ n]h[ n]/ h[ n] h n S n = [− ] = =− = k h[k] 1 h[k] = T{[k]} y[k] x[n] k n =− = { [ ]} = { [ ] [ − ]} n T x k T x n k n = [ ] { [ − ]} n x n T k n = − n x[n]h[k n]

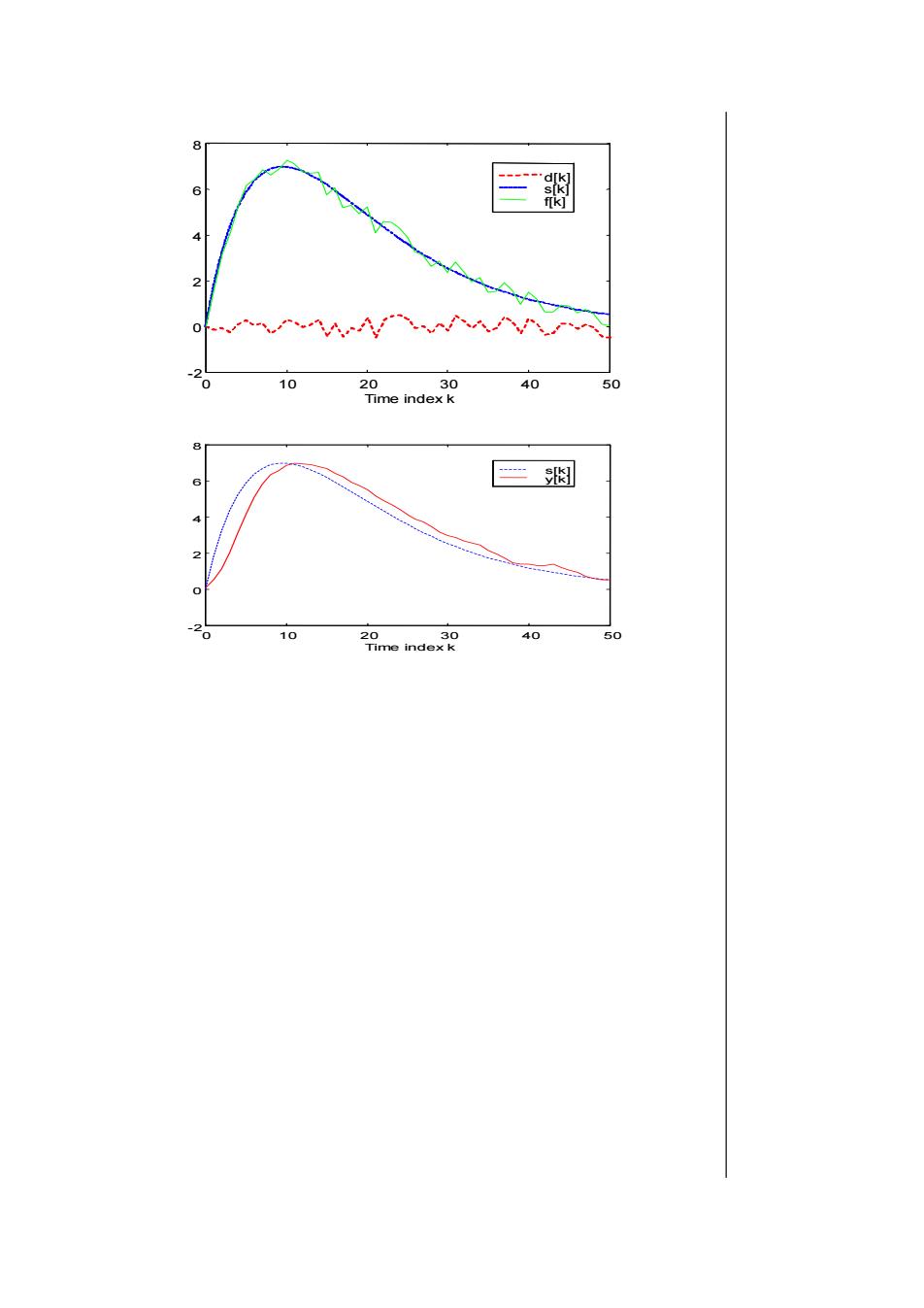
= x[k]*h[k]y[k]= x[k]* h[k]3.用MATLAB求解差分方程描述的离散LTI系统N a,k-- b,[k-n]当N个初始条件和输入已知,就可由下式迭代计算出系统的输出。MN[k]=-(a, /α)y[k-n]+Z ((b, /a)x[k-n]>n=ln=0MATLAB提供了一个filter函数计算由差分方程描述的系统的响应。y=filter(b,a, x )b.a分别表示差分方程的系数。x表示输入序列。y表示输出序列。输出序列的长度和输入序列是相同的。系统的初始条件为零。例:M点的滑动平均(movingaverage)系统定为一[K]=x[k-n]M2受噪声干扰的信号为x [k]=s[k]+d [K]原始信号s[k]-(2k)0.9k噪声d[k]% Signal Smoothing by Moving Average FilterR= 51;%generate (-0.5, 05)Uniformly distributed%random numbersd = rand(1,R)-0.5;k=0:R-1;s=2*k.*(0.9.^k);f=s+d,figure(1), plot(k,d,'r-,k,s,'b--,k,f,'g-),xlabel(Timeindexk'),legend(d[kl,'sk],'fk')M=5; b = ones(M,1)/M; a = 1;y = filter(b,a,f),figure(2); plot(k,s,'b-,k,y,'r-),xlabel(Time index k')legend('s[k],y[k]);
y[k] = x[k]h[k] 3.用 MATLAB 求解差分方程描述的离散 LTI 系统 当 N 个初始条件和输入已知,就可由下式迭代计算出系统的 输出。 MATLAB 提供了一个 filter 函数计算由差分方程描述的系统 的响应。 y=filter(b,a, x ) b,a 分别表示差分方程的系数。 x 表示输入序列。y 表示输出序列。 输出序列的长度和输入序列是相同的。系统 的初始条件为零。 例:M 点的滑动平均(moving average)系统定为 受噪声干扰的信号为 x [k]=s[k]+d [k] 原始信号 s[k]=(2k)0.9k 噪声 d[k] % Signal Smoothing by Moving Average Filter R = 51; %generate (-0.5, 05)Uniformly distributed %random numbers d = rand(1,R)-0.5; k=0:R-1; s=2*k.*(0.9.^k); f=s+d; figure(1); plot(k,d,'r-.',k,s,'b-',k,f,'g-'); xlabel('Time index k'); legend('d[k]','s[k]','f[k]'); M =5; b = ones(M,1)/M; a = 1; y = filter(b,a,f); figure(2); plot(k,s,'b-',k,y,'r-'); xlabel('Time index k'); legend('s[k]','y[k]'); = x[k]*h[k] [ ] [ ] 0 0 a y k n bn x k n M n n N n − = − = = [ ] ( / ) [ ] ( / ) [ ] 0 0 0 1 y k a a y k n bn a x k n M n n N n = − − + − = = [ ] 1 [ ] 1 0 x k n M y k M n = − − =
frkoO1020304050Time indexkP..1030405020Time index k
0 10 20 30 40 50 -2 0 2 4 6 8 Time index k d[k] s[k] f[k] 0 10 20 30 40 50 -2 0 2 4 6 8 Time index k s[k] y[k]

1.3离散时间信号的频域分析1.3.1离散Fourier级数(DFS)DFS的推导周期为N的单位脉冲序定义为3,[K]= S[k-rN]5,[K]x,[K]x4[k] = [k]+ 28,[k -2]一般地,一个周期为N周期序列可表示为N-1[K]=[]%[k-1]1=0-j2元N定义W~=e2wNk是N的整数倍+=N~[K]k不是N的整数倍周期为N的单位脉冲序列DFS表示1 N-1wo%[k] =Nm=o
1.3 离散时间信号的频域分析 1.3.1 离散 Fourier 级数(DFS) DFS 的推导 周期为 N 的单位脉冲序定义为 一般地,一个周期为 N 周期序列可表示为 0 N k 是 N 的整数倍 1 k 不是 N 的整数倍 周期为 N 的单位脉冲序列 DFS 表示 − = − = 1 0 1 [ ] ~ N m km N WN N k [ ] ~ [ ] ~ [ ] ~ 1 0 x k x l k l N N l = − − = [ 2] ~ [ ] 2 ~ [ ] ~ x4 k = 4 k + 4 k − 2 k 0 1 2 3 4 1 [ ] ~ 4 x k 0 1 2 3 4 1 k 5 [ ] [ ] ~ k k rN r N = − =− [ ] ~ 5 k N j N W e 2 − 定义 = − = = 1 0 N l kl WN [ ] ~ = N N k