
x[-n][k]1?kn邓1-n0120123411·n.012x[2 -n][K]*[K]211hk012012周期卷积的矩阵表示x[K]*文,[K]=文[n]x,[k-n]n=0例:N=4[[0]x[0]x[-1]x,[-2] x[-3]][x,[0]]3,[1]x,[1] [1]x,[0]x,[-1] x,[-2][2]x,[2]x,[1],[0]x,[-1]x,[2][[3]x,[3] x,[2]x,[1],[0] [,[3]x,[0],[3],[2],[1],[0]x,[1]x,[0]x,[3]x,[2]x,[1],[2][]x,[0]x,[3],[2][x,[3]x,[2]x,[1]买,[0]x,[3]卷积定理:DFS,[k]*x,[k]=DFS(,[k])DFS[x,[k]]证: DFS([K]*x,[K]= DFS(乏x[n],[k-n]-23[mDF([-~) r=0[nX,[mW”= X[m]X,[m]
0 1 2 k 1 周期卷积的矩阵表示 例:N=4 卷积定理: [ ]} ~ [ ]}DFS{ ~ [ ] DFS{ ~ ~ [ ] ~ DFS 1 2 1 2 x k x k = x k x k = [3] ~ [2] ~ [1] ~ [0] ~ [0] ~ [1] ~ [2] ~ [3] ~ [3] ~ [0] ~ [1] ~ [2] ~ [2] ~ [3] ~ [0] ~ [1] ~ [1] ~ [2] ~ [3] ~ [0] ~ 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 x x x x x x x x x x x x x x x x x x x x 0 1 2 3 k 4 1 1 [ ] ~ x k 0 1 2 n 1 1 [ ] ~ x −n 0 1 2 n 1 1 [1 ] ~ x − n [ ] ~ ~ [ ] ~ x k x k 0 1 2 n 1 1 [2 ] ~ x − n 1 2 [ ] ~ [ ] ~ [ ] ~ ~ [ ] ~ 1 2 1 0 x1 k x2 k x n x k n N n = − − = − − − − − − = [3] ~ [2] ~ [1] ~ [0] ~ [0] ~ [1] ~ [2] ~ [3] ~ [ 1] ~ [0] ~ [1] ~ [2] ~ [ 2] ~ [ 1] ~ [0] ~ [1] ~ [ 3] ~ [ 2] ~ [ 1] ~ [0] ~ [3] ~ [2] ~ [1] ~ [0] ~ 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 x x x x x x x x x x x x x x x x x x x x y y y y − = = − 1 0 1 2 1 2 [ ]} ~ [ ] ~ [ ] DFS{ ~ ~ [ ] ~ : DFS N n 证 x k x k x n x k n − = = − 1 0 1 2 [ ]} ~ [ ]DFS{ ~ N n x n x k n − = = 1 0 1 2 [ ] ~ [ ] ~ N n nm n X m W N x [ ] ~ [ ] ~ = X1 m X2 m

DFS([K]·x[K]=DFS(,[K]] *DFS(3,[K])1-RA左=WIW!1[k]X,[n]nmkNWX,m2x,[KjW(m-m)kNK=0- - =1 DFS(,[K] *DFS(,[K]N1.3.3离散时间Fourier变换(DTFT)DTFT的定义DTFT:X(ej)= Z x[k]e-0n特点:1)X(ejQ)是连续的2)X(ejQ)是周期为2元的周期函数IDTFT:x[k]=-1o X(el")ea d?X(ej°)=[X(ej° )lej(2) = Xr(ej)+ jX,(ejg)(W)的主值(principalvalue)-p<(W)<p例:试求序列x[K]=α'u[K]的 DTFT。解:-jkoXlek=0当a>1时,求和不收敛,DTFT不存在
1.3.3 离散时间 Fourier 变换(DTFT) DTFT 的定义 DTFT: 特点:1)X(e j )是连续的 2)X(e j )是周期为 2 的周期函数 IDTFT: f(W) 的主值(principal value) -p<f(W)p 例: 试求序列 x[k]=a k u[k]的 DTFT。 解: 当|a|>1 时,求和不收敛,DTFT 不存在。 k k k X j 0 j (e ) e − = = ( ) ( ) ( ) ( ) () j I j R j j j X e = X e e = X e + j X e [ ] ~ [ ] 1 ~ 2 1 0 X n X m n N N n = − − = mk N nk N N n N k x k X n W W N − − = − = = [ ] ~ [ ] 1 ~ 1 2 1 0 1 0 [ ]} ~ DFS{ ~ [ ]} ~ DFS{ 1 [ ] ~ [ ] ~ DFS 1 2 1 2 x k x k N x k • x k = − = = 1 0 1 2 [ ] ~ [ ] ~ N k mk WN 左 x k x k m n k N N k N n X n x k W N ( ) 1 1 0 2 1 0 [ ] ~ [ ] 1 ~ − − = − = = [ ]} ~ DFS{ ~ [ ]} ~ DFS{ 1 1 2 x k x k N = j k k j X e x k e − =− ( ) = [ ] x k X e e d j jk ( ) 2 1 [ ] 2 =
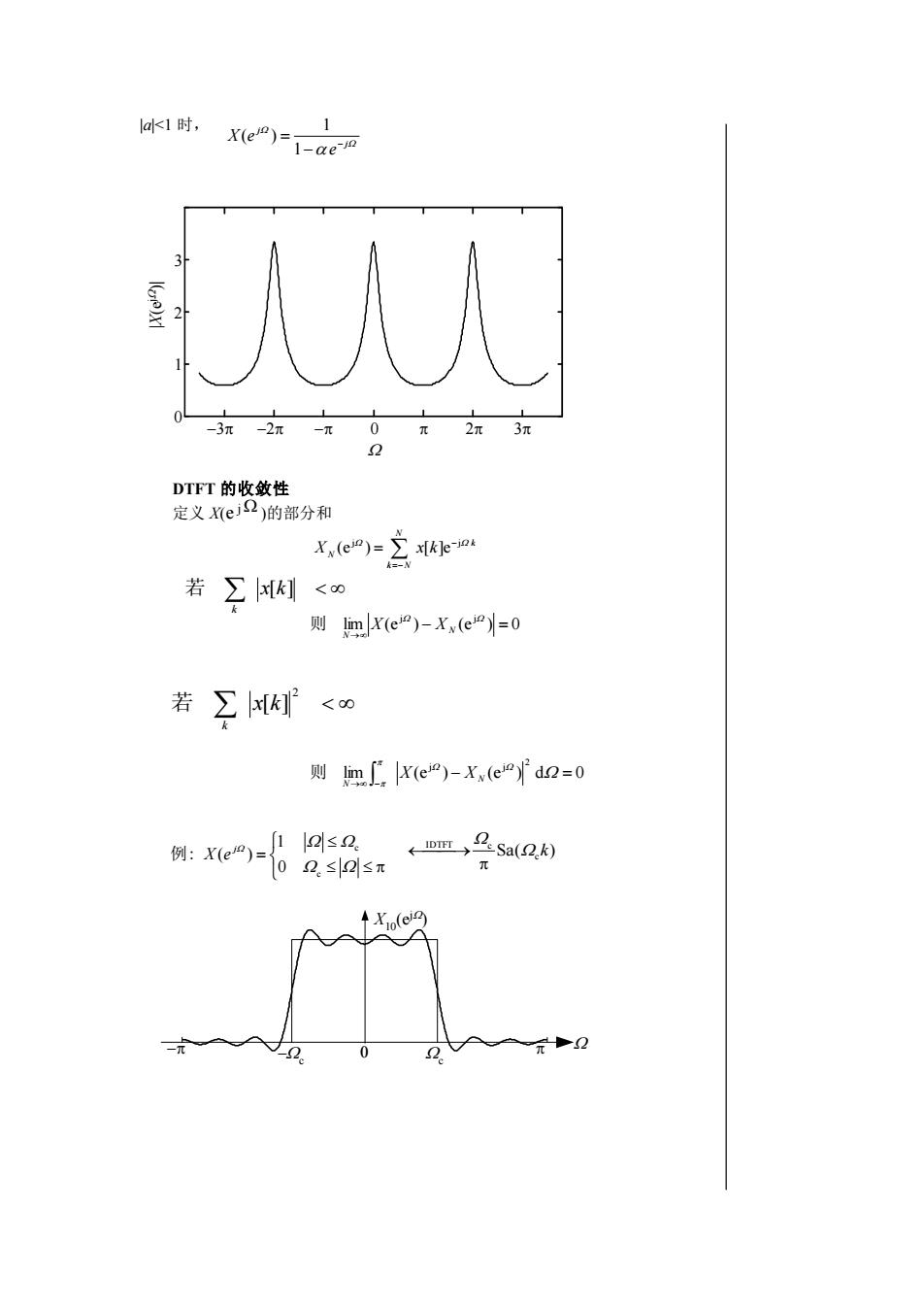
lak<1 时,X(ejn):1-αe-j0人(er0)xl2-2元02元3元-3元元一元2DTFT的收敛性定义X(ej2)的部分和x[k]e-jaXx(ein)= )若≥[]80则 lim|X(ei°)-Xx(ei)=0若[]<8则Jmx(ei)-X(eio)d2=01[≤2,2sSa(2.k)1IDTFT例:X(ejn)=个[02≤2≤元Xio(ei)20(2
|a|<1 时, DTFT 的收敛性 定义 X(e j )的部分和 X10(ej ) − c −c k N k N N X x k j j (e ) [ ]e − =− = 0 3 0 1 2 3 −3 −2 − 2 |X(ej )| j j e X e − − = 1 1 ( ) lim (e ) (e ) 0 j j − = → N N 则 X X x[k] k 若 2 x[k] k 若 lim (e ) (e ) d 0 2 j j − = → − N N 则 X X = c c 0 1 : ( ) j 例 X e Sa( ) c IDTFT c k ⎯⎯→
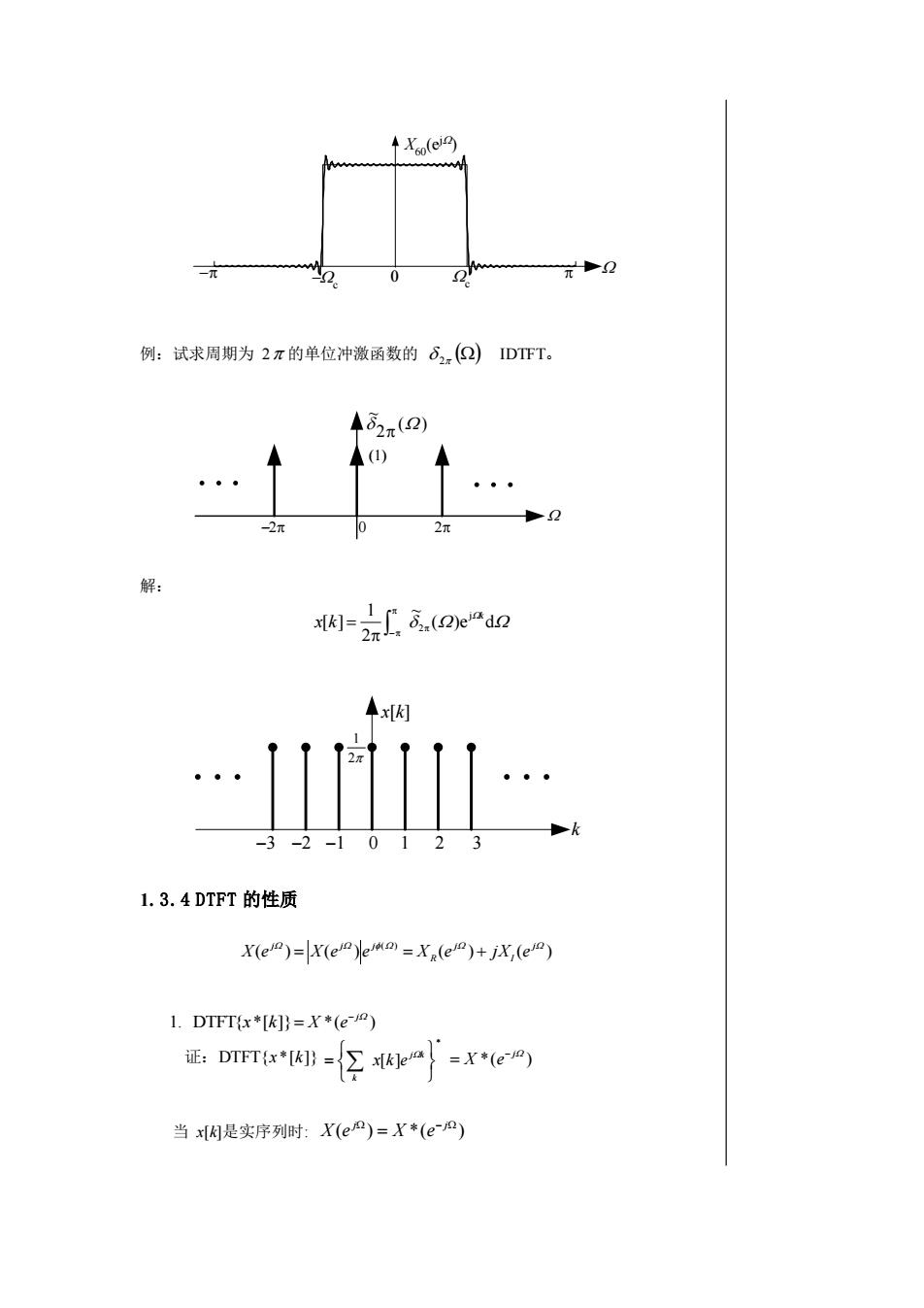
+Xo(ei2)A72例:试求周期为2元的单位冲激函数的82,(Q)IDTFT。432元(2)(1)Q02元-2元解:3.(2)eiad2x[k]=2元x[k]2-3-2-10131.3.4DTFT的性质X(e)=|X(el°)]e() = XR(el°)+ jx,(el°)1. DTFT(x*[K))=X*(e-J2)证: DTFT(x*[K]) ={Z x[k]ea | = X *(e'10)当x[是实序列时:X(ej)=X*(e-j0)
例:试求周期为 2 的单位冲激函数的 () 2 IDTFT。 解: 1.3.4 DTFT 的性质 当 x[k]是实序列时: ( ) *( ) − = j j X e X e x[k] k −2 −1 0 1 2 2 1 −3 3 ( )e d ~ 2 1 [ ] j 2 k x k − = − 0 () ( ) 2 ~ X60(ej ) − c −c ( ) ( ) ( ) ( ) () j I j R j j j X e = X e e = X e + jX e 1. DTFT{ *[ ]} *( ) j x k X e − = 证:DTFT{x *[k]} = j k k x k e [ ] *( ) j X e − =
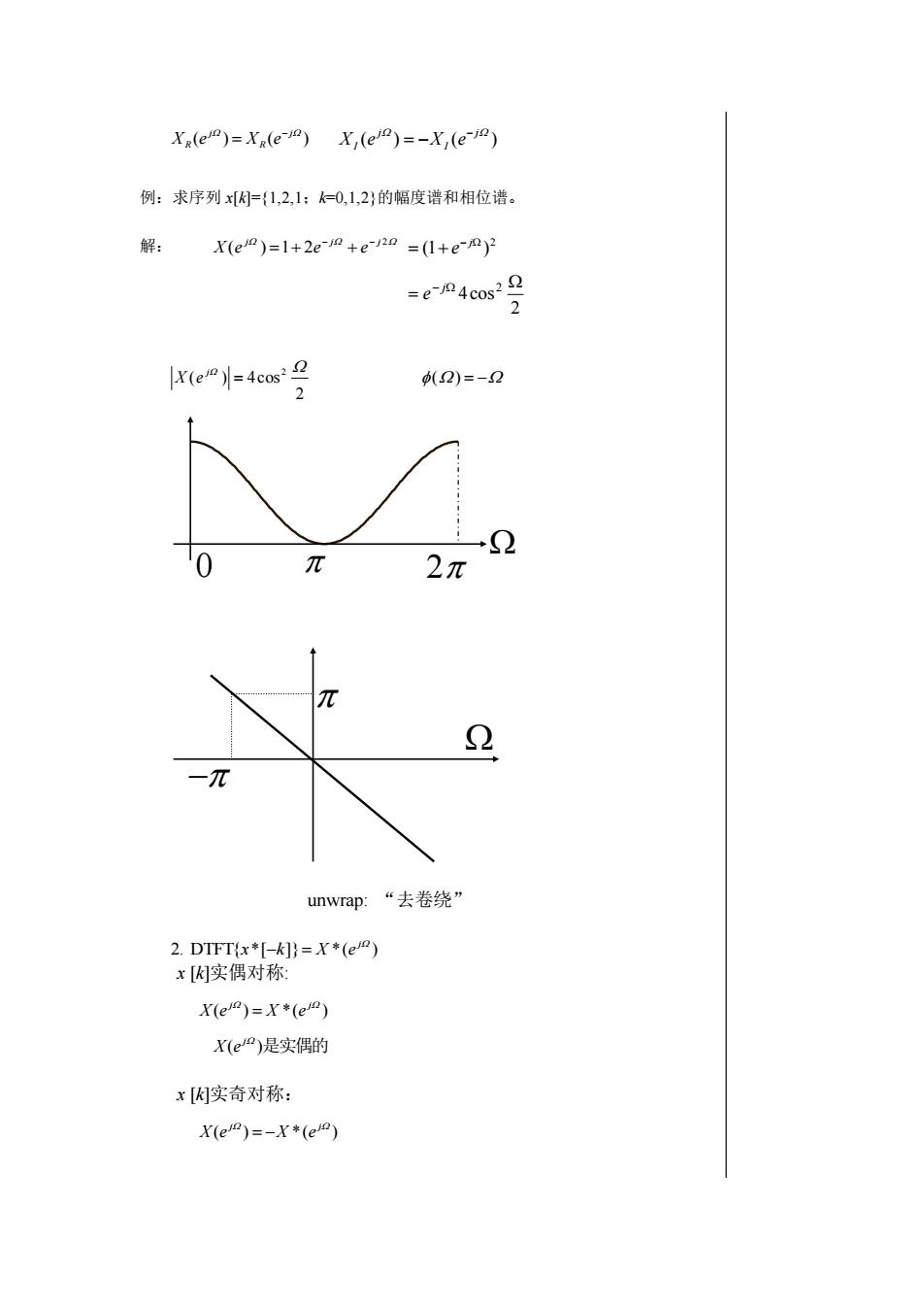
Xr(ej)=Xr(e-j)X(ej)=-X,(e-j2)例:求序列x[K]=(1,2,1;k=0,1,2)的幅度谱和相位谱。解:X(el0)=1+2e-J2 +e-/20 =(1+e-j)2022=e-jn 4cos?2[X(e) =4cos? 2(2)=-22Q0元2 元元2一元“去卷绕”unwrap:2. DTFT(x*[-k])= X*(ej°)x[K]实偶对称:X(ej°)=X*(ej°)X(ej°)是实偶的x[K]实奇对称:X(ej)=-X*(ejn)
例:求序列 x[k]={1,2,1;k=0,1,2}的幅度谱和相位谱。 解: unwrap: “去卷绕” x [k]实偶对称: x [k]实奇对称: − 0 ( ) ( ) j R j R X e X e − = ( ) ( ) j I j I X e X e − = − 2 ( ) 1 2 j j j X e e e − − = + + 2 (1 ) − = + j e 2 4cos2 = − j e 2 ( ) 4cos 2 = j X e () = − 2. DTFT{ *[ ]} *( ) j x −k = X e ( ) *( ) j j X e = X e X(e j )是实偶的 ( ) *( ) j j X e = −X e