
家庭你亚 第2课时 三角形的三条角平分线
第2课时 三角形的三条角平分线

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.三角形的三条角平分线 三角形的三条角平分线相交于一点,并且这一点到三 条边的距离相等 温馨提示 任意三角形的三条角平分线的交点均在三角形的内部. 导航页
导航页 基础自主梳理 1.三角形的三条角平分线 三角形的三条角平分线相交于__________,并且这一点到三 条边的距离__________. 温馨提示 任意三角形的三条角平分线的交点均在三角形的内部. 一点 相等

2.判断下面结论的对错 ()在三角形内部,到三角形三边距离相等的点只有一个 (√) (2)在同一平面内,到三角形三边所在直线距离相等的点只 有一个.(×) (3)三角形的三条角平分线交于一点(√) (4)等腰三角形的底边中点到两腰的距离相等(√) (⑤)三角形是以它的角平分线为对称轴的轴对称图形(×) 导航页
导航页 2.判断下面结论的对错. (1)在三角形内部,到三角形三边距离相等的点只有一个. ( ) (2)在同一平面内,到三角形三边所在直线距离相等的点只 有一个.( ) (3)三角形的三条角平分线交于一点.( ) (4)等腰三角形的底边中点到两腰的距离相等.( ) (5)三角形是以它的角平分线为对称轴的轴对称图形.( ) √ × √ √ ×
核心重难探究 知识点 三角形的三条角平分线的性质的应用 【例题】如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A, ∠B的平分线的交点,试求点P到边AB的距离: B P。 思路点拨:由勾股定理的逆定理可知△ABC是直角三角形,所 以可求出其面积;又由点P是角平分线的交点知点P到三边的 距离都相等,因此连接PA,PB,PC,将△ABC分割成三个小三角 形,利用S△4BCS△PAB+S△PBC+S△P4C可求得点P到边AB的距离 航页
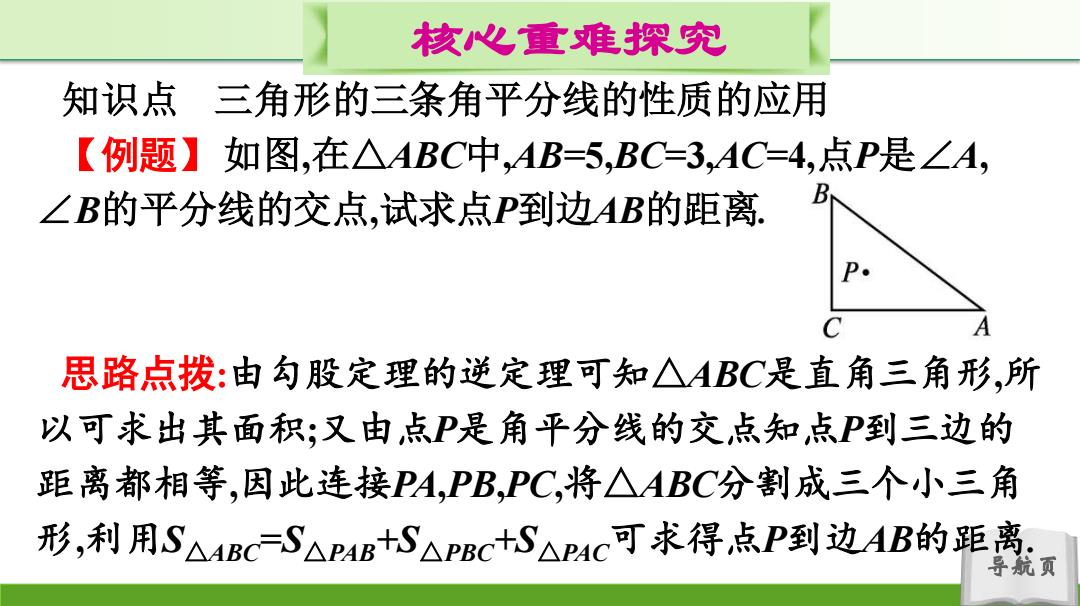
导航页 核心重难探究 知识点 三角形的三条角平分线的性质的应用 【例题】 如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A, ∠B的平分线的交点,试求点P到边AB的距离. 思路点拨:由勾股定理的逆定理可知△ABC是直角三角形,所 以可求出其面积;又由点P是角平分线的交点知点P到三边的 距离都相等,因此连接PA,PB,PC,将△ABC分割成三个小三角 形,利用S△ABC=S△PAB+S△PBC+S△PAC可求得点P到边AB的距离