
家庭值亚 第1课时 一元一次不等式与一次函数的关系
第1课时 一元一次不等式与一次函数的关系

基础自主梳理 导 核心重难探究 航 新知训练织固
导航 基础自主梳理 核心重难探究 新知训练巩固

基础自主梳理 1.一元一次不等式与一次函数的关系 对于一次函数y=kc+b(0): (1)当kx+b>0时y>0,不等式x+b>0的解集就是函数y=r+b (0)的图象在x轴上方 的部分对应自变量x的取值范 围 (2)当x+b<0时,y<0,不等式c+b<0的解集就是函数 y=c+b(0)的图象在x轴下方 的部分对应自变量x的 取值范围; (3)当x+b=0时y=0,方程kc+b=0的解就是函数y=kc+b(0) 的图象与x轴交点的横坐标 导航页
导航页 基础自主梳理 1.一元一次不等式与一次函数的关系 对于一次函数y=kx+b(k≠0): (1)当kx+b>0时,y>0,不等式kx+b>0的解集就是函数y=kx+b (k≠0)的图象在x轴__________的部分对应自变量x的取值范 围; (2)当kx+b<0时,y<0,不等式kx+b<0的解集就是函数 y=kx+b(k≠0)的图象在x轴__________的部分对应自变量x的 取值范围; (3)当kx+b=0时,y=0,方程kx+b=0的解就是函数y=kx+b(k≠0) 的图象与x轴交点的__________. 上方 下方 横坐标

2.已知函数y=8x-11,要使y>0,则x应取(A) A11 8 Br<11 8 C.x>0 D.x<0 导航页
导航页 2.已知函数 y=8x-11,要使 y>0,则 x 应取( ). A.x> 𝟏𝟏 𝟖 B.x< 𝟏𝟏 𝟖 C.x>0 D.x<0 A
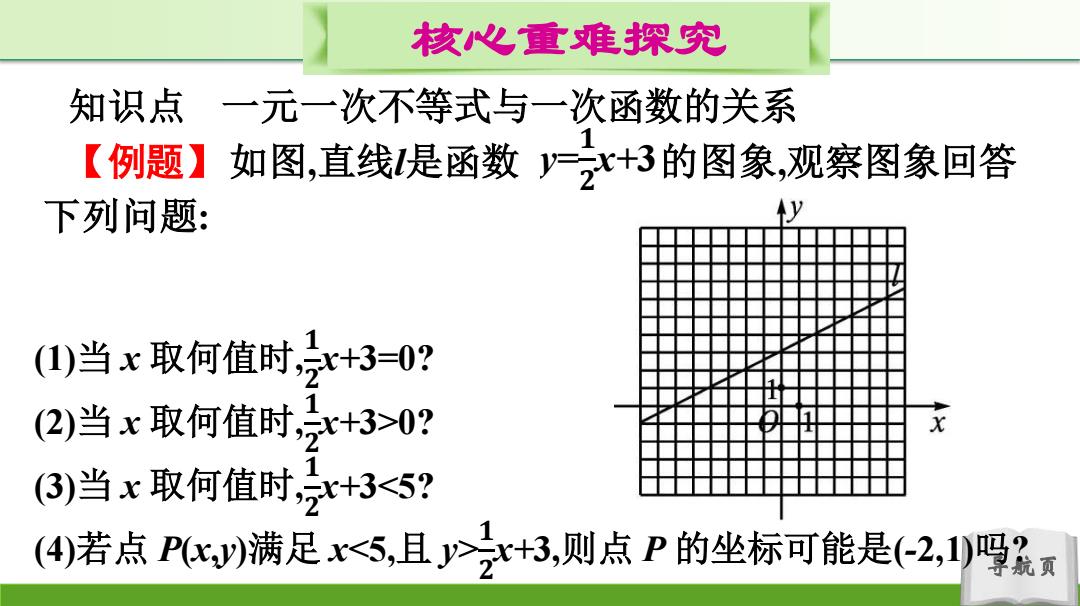
核心重难探究 知识点 一元一次不等式与一次函数的关系 【例题】如图,直线是函数一式+3的图象,观察图象回答 下列问题: (1)当x取何值时,2+3=0? (2)当x取何值时,x+3>0? (3)当x取何值时,x+3<5? (④)若点Pc)满足x5,且式+3,则点P的坐标可能是(-2,1)吗最
导航页 核心重难探究 知识点 一元一次不等式与一次函数的关系 【例题】如图,直线l是函数 的图象,观察图象回答 下列问题: y= 𝟏 𝟐 x+3 (1)当 x 取何值时, 𝟏 𝟐 x+3=0? (2)当 x 取何值时, 𝟏 𝟐 x+3>0? (3)当 x 取何值时, 𝟏 𝟐 x+3<5? (4)若点 P(x,y)满足 x<5,且 y> 𝟏 𝟐 x+3,则点 P 的坐标可能是(-2,1)吗?