
几种不同阳值时的旋转因子 + 2 元 π cos *sm2=+ 2 。=cow孕+jsi讽-7=-j 0=士元,e生x=cos(±冗)+jsin(仕)=-1 故+j,-j,一1都可以看成旋转因子
e j j j = + = + = 2 sin 2 cos , 2 2 e j j j = − + − = − = − − ) 2 ) sin( 2 , cos( 2 2 = , = cos() + sin() = −1 e j j 故 +j, –j, -1 都可以看成旋转因子。 几种不同值时的旋转因子 Re Im 0 I + jI jI − I −
8.2正弦量 1.正弦量 瞬时值表达式: 波形: i(t)=Imc0s(ot什W 正弦量为周期函数 t)=f(t什kT 1 周期T(period和频率f(frequency): T 周期T:重复变化一次所需的时间。 单位:S,秒 频率f:每秒重复变化的次数。 单位:Hz,赫(兹)
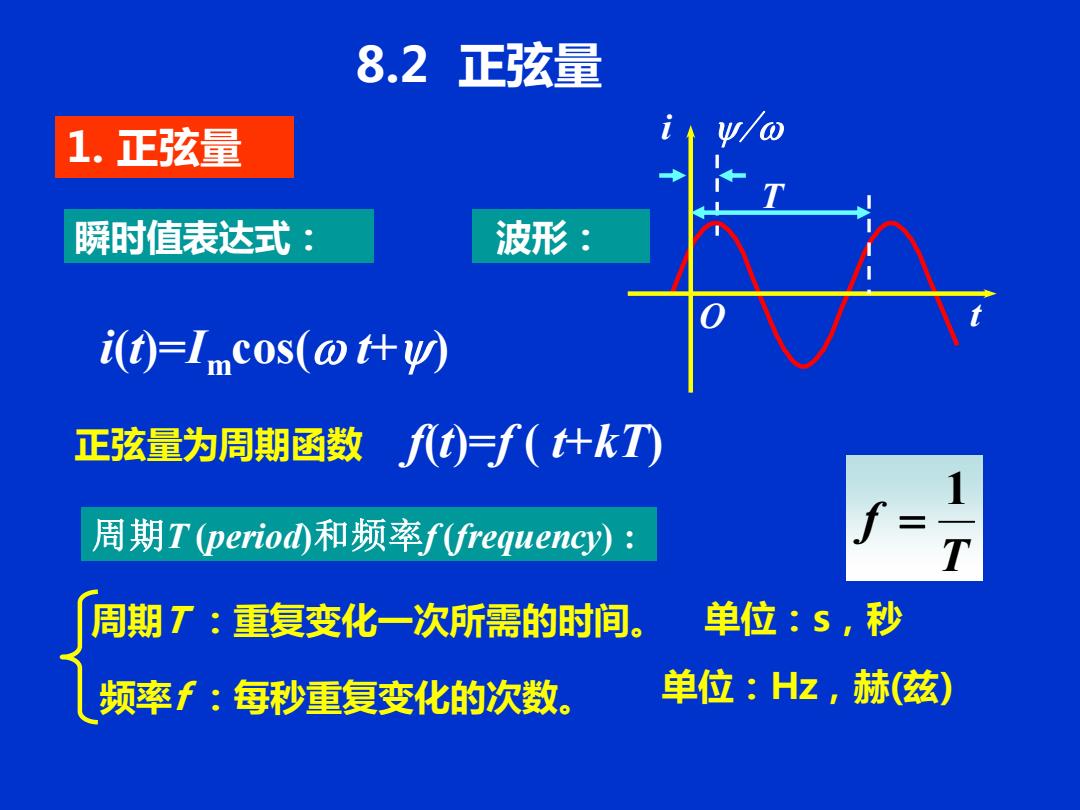
8.2 正弦量 1. 正弦量 瞬时值表达式: i(t)=Imcos(w t+y) 波形: t i O y/w T 周期T (period)和频率f(frequency) : 频率f :每秒重复变化的次数。 周期T :重复变化一次所需的时间。 单位:Hz,赫(兹) 单位:s,秒 T f 1 = 正弦量为周期函数 f(t)=f ( t+kT)

●正弦交流电路 激励和响应均为正弦量的电路 (正弦稳态电路)称为正弦电路 或交流电路。 研究正弦电路的意义: (1)正弦稳态电路在电力系统和电子技术领域占有十分重 要的地位。 优点: 1)正弦函数是周期函数,其加、减、求导、积分 运算后仍是同频率的正弦函数 2)正弦信号容易产生、传送和使用
⚫ 正弦交流电路 激励和响应均为正弦量的电路 (正弦稳态电路)称为正弦电路 或交流电路。 (1)正弦稳态电路在电力系统和电子技术领域占有十分重 要的地位。 ⚫ 研究正弦电路的意义: 1)正弦函数是周期函数,其加、减、求导、积分 运算后仍是同频率的正弦函数 优点: 2)正弦信号容易产生、传送和使用

(2)正弦信号是一种基本信号,任何变化规律复杂的信号 可以分解为按正弦规律变化的分量。 f(t)=∑A cos(kot+日:) k=1 对正弦电路的分析研究具有重要的理论 价值和实际意义
(2)正弦信号是一种基本信号,任何变化规律复杂的信号 可以分解为按正弦规律变化的分量。 ( ) cos( ) 1 k n k k f t = A kwt + = 对正弦电路的分析研究具有重要的理论 价值和实际意义
2.正弦量的三要素 i(t)=Imcos(ot什y (1)幅值(amplitude))(振幅、最大值)lm 反映正弦量变化幅度的大小。 (2)角频率(angular frequency)W 相位变化的速度,反映正弦量变化快慢。 @=2mf=27 单位:rad/s, 弧度/秒 (3)初相位(initial phase angle)y 反映正弦量的计时起点, 2π @t 常用角度表示
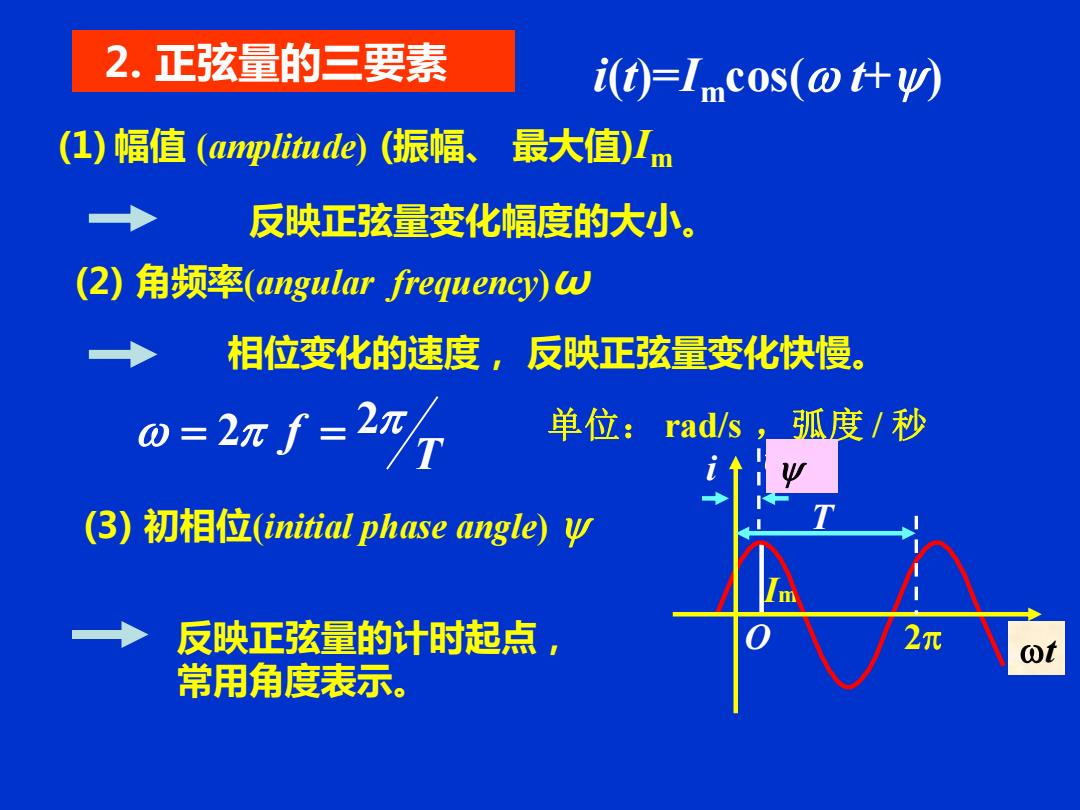
(1) 幅值 (amplitude) (振幅、 最大值)Im (2) 角频率(angular frequency)ω 2. 正弦量的三要素 (3) 初相位(initial phase angle) y Im 2 y/w t i O T wt T w = 2 f = 2 单位: rad/s ,弧度 / 秒 反映正弦量变化幅度的大小。 相位变化的速度, 反映正弦量变化快慢。 反映正弦量的计时起点, 常用角度表示。 i(t)=Imcos(w t+y) y